Pierwiastek sześcienny

Pierwiastkiem sześciennym liczby jest taka liczba że . Pierwiastki sześcienne oznacza się symbolem [1]. Liczbę nazywa się liczbą podpierwiastkową. Rozważa się pierwiastki sześcienne z liczb rzeczywistych oraz zespolonych . Pojęcie pierwiastkowania rozszerza się także na elementy dowolnych pierścieni przemiennych, przy czym pierwiastki (w tym sześcienne) definiuje się w analogiczny sposób, jak to zdefiniowane jest dla liczb.
Pierwiastki z liczb rzeczywistych
Liczby rzeczywiste mają zawsze pojedyncze pierwiastki sześcienne w dziedzinie liczb . Tj. dla dowolnej liczby rzeczywistej istnieje tylko jedna liczba rzeczywista taka, że .

Jest tak dlatego, że funkcja sześcienna , do której funkcja pierwiastka sześciennego jest odwrotna, jest rosnąca w całym zakresie liczb rzeczywistych i dla dwóch różnych wartości daje różne wyniki . Innymi słowy, funkcja sześcienna jest bijekcją (odwzorowuje zbiór liczb rzeczywistych na zbiór liczb rzeczywistych w relacji 1 do 1). Dlatego też można zdefiniować funkcję odwrotną, która każdej liczbie rzeczywistej przyporządkowuje unikalny pierwiastek sześcienny.
Pierwiastek sześcienny w dziedzinie liczb rzeczywistych z liczby dodatniej jest liczbą dodatnią, a z liczby ujemnej jest liczbą ujemną, np. , gdyż ; , gdyż .
Twierdzenia
- Pierwiastek sześcienny z liczby naturalnej jest liczbą naturalną wtedy i tylko wtedy, gdy liczba pierwiastkowana jest sześcianem liczby naturalnej[2]. Na przykład jest liczbą niewymierną.
- W twierdzeniu powyższym liczby naturalne można zastąpić liczbami całkowitymi.
- Pierwiastek sześcienny z liczby wymiernej jest liczbą wymierną wtedy i tylko wtedy, gdy liczba podpierwiastkowa jest sześcianem liczby wymiernej.
- Dla każdej liczby rzeczywistej istnieje dokładnie jeden rzeczywisty pierwiastek sześcienny z Wynika to z tego, że funkcja
- dla
- jest ciągłą funkcją rosnącą oraz oraz
- Z wartości granic na podstawie twierdzenia Darboux wynika wtedy, że funkcja ta przekształca zbiór liczb rzeczywistych na a z monotoniczności wynika jej różnowartościowość. Dlatego dla każdej liczby istnieje dokładnie jedna liczba Liczba jest pierwiastkiem sześciennym z
Tożsamości - pierwiastek sześcienny z liczb rzeczywistych
Z definicji pierwiastka sześciennego i definicji potęgi wynika tożsamość (por. Potęgowanie)
Z własności potęgowania wynikają następujące tożsamości:
- - pierwiastek sześcienny z liczby przeciwnej (szczególny przypadek tożsamości podanej niżej)
- dla
Tożsamości dla sumy i różnicy pierwiastków sześciennych:
Pierwiastki z liczb zespolonych
Liczby zespolone mają zawsze trzy pierwiastki sześcienne. Gdy liczba zespolona redukuje się do liczby rzeczywistej (tj. ma tylko niezerową część rzeczywistą, a zerową część urojona), to i tak liczba ta ma trzy pierwiastki w dziedzinie liczb zespolonych : jeden rzeczywisty pierwiastek sześcienny oraz parę zespolonych, sprzężonych pierwiastków sześciennych; natomiast liczby zespolone o niezerowej części urojonej mają trzy różne zespolone pierwiastki sześcienne (por. wykresy pierwiastków zespolonych liczb oraz ). Na płaszczyźnie zespolonej pierwiastki sześcienne liczby znajdują się na wierzchołkach trójkąta równoramiennego, obróconego o kat względem osi rzeczywistej, gdzie - argument danej liczby (por. poniżej).

Wzory na obliczanie pierwiastków zespolonych
Jeżeli liczbę zespoloną zapisze się w postaci wykładniczej
- ,
to jej trzy pierwiastki sześcienne oblicza się ze wzoru de Moivre’a[3]
Równoważny zapis (korzystający z postaci trygonometrycznej liczby zespolonej)[4]
Pierwiastki sześcienne z jedynki a pierwiastki dowolnej liczby
Dla liczby 1 moduł i argument wynoszą odpowiednio Licząc ze wzoru de Moivre'a pierwiastki sześcienne otrzymamy:
Z wzoru de Moivre'a wynika, że dla dowolnej liczby zespolonej jej pierwiastki sześcienne dane są wzorami:
Wynika stąd, że pierwiastki oraz można otrzymać mnożąc pierwiastek przez drugi i trzeci pierwiastek z jedynki, tj.
Jeżeli oznaczymy
Wtedy
W ogólności pierwiastki sześcienne dowolnej liczby można zapisać w zwartej formule:
gdzie oznacza tu dowolny z trzech pierwiastków zespolonych danej liczby.
Wzór ten oznacza, że pozostałe pierwiastki otrzymuje się przez mnożenie danego pierwiastka przez pierwiastek z jedynki i jego kwadrat . Na płaszczyźnie zespolonej odpowiada to obrotowi wektora wodzącego punktu, wyznaczającego położenie pierwiastka , o kąty
Pierwiastki zespolone liczb rzeczywistych i problem zmiany numeracji

Pierwiastki obliczone wg wzoru de Moivre'a dla liczby mają wartości (moduł i argument wynoszą odpowiednio ):
- .
Gdyby jednak jako wartość startową przyjąć czyli wartość pierwiastka rzeczywistego (tj. zdefiniowanego w dziedzinie liczb rzeczywistych), to np. dla liczby mielibyśmy wg wyżej podanej reguły następującą kolejność pierwiastków:
czyli pierwiastek zerowy wg wzoru de Moivre'a stałby się ostatnim wg drugiej reguły obliczeń, itd. Kolejność numeracji pierwiastków w obliczeniach może być istotna. Stąd m. in. powstała potrzeba definicji pierwiastka głównego, co omówiono niżej.
Pierwiastek zespolony główny
Skoro w dziedzinie liczb zespolonych pierwiastek ma wiele wartości (w tym trzy dla pierwiastka sześciennego), to wprowadza się pojęcie tzw. pierwiastka głównego, który definiuje się jako pierwiastek, który ma największą wartość bezwzględna części rzeczywistej, lub - równoważnie - jako mający najmniejszą wartość bezwzględną argumentu, tj. jeżeli liczbę zespoloną przedstawi się w postaci wykładniczej[4]
- ,
przyjmując , to pierwiastek główny wynosi
Pierwiastek główny jest więc pierwiastkiem o numerze 0 wg wzoru de Moivre'a, gdy ustali się fazę liczby zespolonej w przedziale .
Konsekwencją takiej definicji jest, że pierwiastek główny jest dla liczb ujemnych liczbą zespoloną; np. dla liczby jest równy , a nie , czyli pierwiastek główny sześcienny w dziedzinie liczb zespolonych jest różny od pierwiastka sześciennego w zbiorze liczb rzeczywistych. (Dla liczb dodatnich pierwiastek główny jest identyczny z pierwiastkiem arytmetycznym.)
Pierwiastek sześcienny na powierzchni Riemanna
Ponieważ pierwiastek z liczby zespolonej ma wiele wartości, to nie da się bezpośrednio utworzyć funkcji, która jednoznacznie przyporządkowuje liczbie zespolonej pierwiastek sześcienny . Tę trudność można rozwiązać rozważając funkcje wielowartościowe, pisząc wyjściową liczbą zespoloną w trzech postaciach
Wtedy pierwiastki główne tych trzech postaci mają wartości (por. pierwiastkowanie liczb zespolonych - Wzór de Moivre’a):
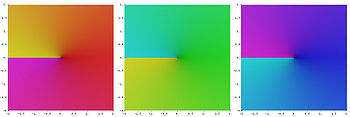
Trzy części powierzchni Riemanna, na których umieszcza się poszczególne trzy pierwiastki sześcienne w zbiorze liczb zespolonych; pierwszy obrazek pokazuje główną część, na której umieszczone są pierwiastki główne, zdefiniowane w tym artykule.
Teoretycznie uzasadnia się to budując za pomocą przedłużenia analitycznego powierzchnię Riemanna, na której można określić pierwiastek sześcienny jako funkcję. Powierzchnię tę można sobie wyobrazić jako trzy egzemplarze płaszczyzny zespolonej z usuniętym punktem 0 i rozcięciem wzdłuż półprostych wychodzących z punktu 0 i połączone z sobą tak, jak jest to pokazane na rysunku.
Różne języki obliczeniowe przyjmują stosowne definicje pierwiastków głównych.
Pierwiastek sześcienny w algebrze
Z algebraicznego punktu widzenia pierwiastkiem sześciennym jest dowolne rozwiązanie równania zmiennej (czyli pierwiastek wielomianu ). Równania takie można rozpatrywać nad dowolnym pierścieniem przemiennym, analogicznie jak w dziedzinie liczb rzeczywistych i zespolonych.
Metoda iteracyjna Newtona

Metoda Newtona jest metodą iteracyjną, którą można użyć do obliczania pierwiastka sześciennego w dziedzinie liczb R. W zerowym kroku zadaje się wartość startową (np.), w kolejnych krokach oblicza się coraz lepsze przybliżenia pierwiastka sześciennego z liczby , przy czym :
Obok pokazano kolejne przybliżenia obliczeń pierwiastka sześciennego z liczby , zaczynając od wartości początkowej (bardzo dalekiej od wartości dokładnej); pomimo tego już w 14-tym kroku uzyskano wynik z dokładnością do . Pokazuje to, jak skuteczna jest to metoda.
O potrzebie odróżniania dziedzin R i C w obliczeniach
Dana liczba ma jedną wartość pierwiastka sześciennego w dziedzinie liczb rzeczywistych (jeżeli pierwiastek istnieje), ale trzy wartości pierwiastka w dziedzinie liczb zespolonych. Jest to istotne rozróżnienie, gdyż np. liczenie numeryczne pierwiastków może prowadzić do błędów, jeżeli zamiast pierwiastka w dziedzinie liczb rzeczywistych zostanie przyjęty jako wynik jeden z pierwiastków z dziedziny liczb zespolonych. (Patrz np. omówienie problemu liczenia pierwiastków równania sześciennego wg wzorów Cardana). Ta sama uwaga dotyczy liczenia pierwiastków wyższych stopni: w dziedzinie liczb zespolonych pierwiastek n-tego stopnia ma n różnych wartości dla danej liczby.
Liczenie pierwiastków sześciennych w językach programowania
W obliczeniach numerycznych konieczna jest uwaga: czy zastosowana procedura danego języka programowania liczy np. pierwiastek sześcienny główny w dziedzinie zespolonej czy pierwiastek w dziedzinie rzeczywistej. Przykładowo: w języku Python do liczenie pierwiastków rzeczywistych 3-go stopnia z liczby m nie należy używać funkcji cmath.pow(m, 1/3) z biblioteki cmath lub instrukcji m**(1/3) , gdyż dla liczb ujemnych otrzyma się jako wynik główny pierwiastek zespolony (wg wyżej podanej definicji), a nie pierwiastek sześcienny w dziedzinie liczb rzeczywistych (np. dla zamiast otrzyma się liczbę ), co prowadzi do błędnych wyników. W Python można zaś użyć funkcji cbrt (cubic root) z biblioteki numpy, co daje poprawnie liczbę rzeczywistą lub napisać własny, krótki kod:
if m>0: u=m**(1/3) else: u=-(-m)**(1/3)

Dodatek: Obliczanie pierwiastka sześciennego prymitywnym kalkulatorem
Korzystając z zależności[a]
można zastosować następujący algorytm obliczania pierwiastka sześciennego dysponując kalkulatorem wyposażonym w klawisz do obliczania tylko pierwiastka kwadratowego i mnożenia, rozpoczynając go po uzyskaniu na wyświetlaczu liczby, z której chcemy obliczyć pierwiastek sześcienny.
- Wykonaj jeden raz pierwiastkowanie.
- Wykonaj mnożenie.
- Wykonaj dwa razy pierwiastkowanie.
- Wykonaj mnożenie.
- Wykonaj cztery razy pierwiastkowanie.
- Wykonaj mnożenie.
- Wykonaj osiem razy pierwiastkowanie.
- Wykonaj mnożenie....
Proces należy kontynuować, aż liczba przestanie się zmieniać po naciśnięciu klawisza mnożenia, ponieważ powtarzana operacja pierwiastkowania wynosi 1 (co oznacza, że rozwiązanie zostało osiągnięte z największą dokładnością jaką ten kalkulator mógł osiągnąć). A następnie:
- Naciśnij ostatni raz klawisz pierwiastkowania.
W tym momencie na wyświetlaczu pojawi się przybliżona wartość pierwiastka sześciennego.
Objaśnienie metody
Podnosząc do potęgi po obu stronach tożsamości powyżej otrzymujemy:
- (*)
Z lewej strony równania mamy pierwiastek sześcienny z
Po 2, 4, 6, 8, ... krokach obliczeń przybliżenia wartości pierwiastka sześciennego wynoszą :
, , , , itd.
Im więcej kroków zrobi się, tym lepsze przybliżenie.
Metoda alternatywna
Powyższa metoda wymaga aby kalkulator był wyposażony w funkcję pierwiastka kwadratowego. Dysponując prostą metodą obliczania pierwiastka kwadratowego następujące wyrażenie jest szybko zbieżne do wyniku:
Gdzie z każdą iteracją wynik jest zbieżny do pierwiastka sześciennego z
Ta metoda wymaga mniej iteracji niż metoda Halleya, ale wymaga więcej obliczeń, ukrytych w wyznaczeniu pierwiastków kwadratowych. Z uwagi na szybką zbieżność, początkowe przybliżenie wartością 1 jest wystarczające.
Przykładowe wartości
Historia

Na temat obliczania pierwiastków sześciennych można znaleźć wzmianki u matematyków babilońskich(inne języki) z 1800 r. B.C.[5] W IV wieku B.C. Platon postawił problem podwojenia objętości sześcianu za pomocą klasycznej konstrukcji (tj. z użyciem cyrkla i linijki), co wymaga wyznaczenia długości krawędzi nowego sześcianu o długości raza większej od krawędzi pierwotnego sześcianu (obecnie wiadomo, że konstrukcja taka jest niemożliwa). Metoda wyodrębniania pierwiastków sześciennych pojawiła się następnie w dziele Dziewięć rozdziałów o sztuce matematycznej 九章算术(inne języki), chińskim(inne języki) tekście matematycznym skompilowanym około II w. B.C.[6] Grecki matematyk(inne języki) Heron z Aleksandrii opracował metodę obliczania pierwiastków sześciennych w pierwszym wieku naszej ery. Jego formuła została ponownie wspomniana przez Eutokiosa w komentarzu do Archimedesa.[7] W 499 n.e Aryabhata opisał metodę znajdowania pierwiastków sześciennych z liczb wielocyfrowych w swoim dziele Aryabhatiya (rozdział 2.5)[8].
Zobacz też
- pierwiastkowanie
- pierwiastek kwadratowy
- pierwiastek z jedynki
- podwojenie sześcianu
- pierwiastkowanie liczb zespolonych - Wzór de Moivre’a.
- algorytm obliczania pierwiastka n-tego stopnia
Inne:
- równanie sześcienne - praktyczny przykład liczenia pierwiastków sześciennych i związane z tym subtelności
Uwagi
- ↑ Dowód tożsamości Aby obliczyć prawą stronę tożsamości należy wyznaczyć wartość iloczynu nieskończonego
Przypisy
- ↑ pierwiastek sześcienny, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2023-08-27] .
- ↑ Sierpiński 1968 ↓, s. 244.
- ↑ Trajdos 1993 ↓, s. 69.
- ↑ a b Trajdos 1993 ↓, s. 70.
- ↑ H.W.F.H.W.F. Saggs H.W.F.H.W.F., Civilization Before Greece and Rome, Yale University Press, 1989, ISBN 978-0-300-05031-8 .
- ↑ JohnJ. Crossley JohnJ., Anthony W.-C.A.W.C. Lun Anthony W.-C.A.W.C., The Nine Chapters on the Mathematical Art: Companion and Commentary, Oxford University Press, 1999, ISBN 978-0-19-853936-0 .
- ↑ J. GilbartJ.G. Smyly J. GilbartJ.G., Heron's Formula for Cube Root, „Hermathena”, 42, 19, Trinity College Dublin, 1920, s. 64–67 .
- ↑ Aryabhatiya (marathi), Mohan Apte, Pune, India, Rajhans Publications, 2009, p. 62, ISBN 978-81-7434-480-9.
Bibliografia
- WacławW. Sierpiński WacławW., Arytmetyka teoretyczna, wyd. 4, Warszawa: Państwowe Wydawnictwo Naukowe, 1968 .
- T.T. Trajdos T.T., Matematyka, cz. III, Warszawa: PWN, 1993, s. 69-73, ISBN 83-204-1547-0 .
Linki zewnętrzne
- Computing the Cube Root, K. Turkowski, Apple Technical Report #KT-32, 1998. (ang.) Zawiera kod źródłowy w C.
- Pierwiastek sześcienny na PlanetMath.
- Eric W.E.W. Weisstein Eric W.E.W., Pierwiastek sześcienny, [w:] MathWorld, Wolfram Research (ang.).
- p
- d
- e
| algebraiczne |
| ||||||
|---|---|---|---|---|---|---|---|
| przestępne |
| ||||||
| krzywe tworzące wykresy |
| ||||||
| powiązane tematy |
- Britannica: topic/cube-root
- SNL: kubikkrot
- DSDE: kubikrod
![{\displaystyle y={\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be50c0a49b200fb46800951d0268b0a9d4e3fdda)



![{\displaystyle {\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a55f866116e7a86823816615dd98fcccde75473)



![{\displaystyle {\sqrt[{3}]{8}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f378331b0d609846c021c1a0bbff0a4fc1755c3)

![{\displaystyle {\sqrt[{3}]{-8}}=-2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b130ad49972cfb951cd0334b8fce072ad343026)

![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)











![{\displaystyle {\sqrt[{3}]{x}}\equiv x^{{1}/{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52b4b894ae9ab70fd3c1fdcf1c8586ae6cd7f755)
![{\displaystyle {\sqrt[{3}]{x^{m}}}=\left({\sqrt[{3}]{x}}\right)^{m}=\left(x^{1/3}\right)^{m}=x^{m/3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb65f4021359e27b70c5f9593403b0e9b99482a1)
![{\displaystyle \left({\sqrt[{3}]{x}}\right)^{3}=x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21ec18fc45aa08e653a9c21432184bc7ff422b0b)

![{\displaystyle {\sqrt[{3}]{-x}}=-{\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb5e141a3ffde34ff9af892e7edfa693d7810684)
![{\displaystyle {\sqrt[{3}]{xy}}={\sqrt[{3}]{x}}{\sqrt[{3}]{y}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11b28085a8ce5f14dfe5b311ef875c09994ab47a)
![{\displaystyle {\sqrt[{3}]{x/y}}={\frac {\sqrt[{3}]{x}}{\sqrt[{3}]{y}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89f5c5a2ddbbcabf8268772d518338236330501b)

![{\displaystyle {\sqrt[{3}]{a}}+{\sqrt[{3}]{b}}={\sqrt[{3}]{a+b+3{\sqrt[{3}]{a^{2}b}}+3{\sqrt[{3}]{ab^{2}}}}}={\frac {a+b}{{\sqrt[{3}]{a^{2}}}-{\sqrt[{3}]{ab}}+{\sqrt[{3}]{b^{2}}}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d252bbf9dd07ee3b911172354c71ac1045fc49a0)
![{\displaystyle {\sqrt[{3}]{a}}-{\sqrt[{3}]{b}}={\sqrt[{3}]{a-b-3{\sqrt[{3}]{a^{2}b}}+3{\sqrt[{3}]{ab^{2}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/926d3a9ec079e8fa8be53a859d104b1d0b7832ba)






![{\displaystyle t_{k}\equiv {\sqrt[{3}]{z}}_{(k)}={\sqrt[{3}]{|z|}}\cdot e^{i(\phi +2\pi \cdot k)/3},\ k\in \{0,1,2\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef4546861978f8c04662e47d22be8229b5a6d4a8)
![{\displaystyle t_{k}\equiv {\sqrt[{3}]{z}}_{(k)}={\sqrt[{3}]{|z|}}\cdot {\big [}\cos {\big (}{\tfrac {\varphi +2k\pi }{3}}{\big )}+i\sin {\big (}{\tfrac {\varphi +2k\pi }{3}}{\big )}{\big ]},\quad k\in \{0,1,2\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c43b97c3e2c2444dc67b9172510a2b9c7fdd8a5)

![{\displaystyle {\sqrt[{3}]{1}}={\begin{cases}e^{i{\frac {2\pi }{3}}\cdot 0}=1\\e^{i{\frac {2\pi }{3}}\cdot 1}=-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}={\frac {-1+i{\sqrt {3}}}{2}}\\e^{i{\frac {2\pi }{3}}\cdot 2}=-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}={\frac {-1-i{\sqrt {3}}}{2}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86564cf64c100554650c320a6cd4f8d1f66e4f7d)
![{\displaystyle t_{0}={\sqrt[{3}]{|z|}}\cdot e^{i(\phi +2\pi \cdot 0)/3}={\sqrt[{3}]{|z|}}\cdot e^{i\phi /3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fad24b3740a04e7b9999e9bf8d68604c5c57a79e)
![{\displaystyle t_{1}={\sqrt[{3}]{|z|}}\cdot e^{i(\phi +2\pi \cdot 1)/3}={\sqrt[{3}]{|z|}}\cdot e^{i\phi /3}e^{i2\pi /3}=t_{0}e^{i2\pi /3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9139d3f90f7025c81e45110be9609a3d2dae2412)
![{\displaystyle t_{2}={\sqrt[{3}]{|z|}}\cdot e^{i(\phi +2\pi \cdot 2)/3}={\sqrt[{3}]{|z|}}\cdot e^{i\phi /3}e^{i4\pi /3}=t_{0}e^{i4\pi /3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13b7d80fe39cec0d5129d45a81b8c1b898fad2bc)







![{\displaystyle {\sqrt[{3}]{z}}={\begin{cases}t_{0}\\t_{1}=t_{0}\cdot \omega \\t_{2}=t_{0}\cdot \omega ^{2}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8eaf703accd6a00526099840790d01253f3cdb5)







![{\displaystyle t_{0}={\sqrt[{3}]{|z|}}\cdot e^{i\phi /3}=2\cdot e^{i\pi /3}=1+i{\sqrt {3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9b54be7357e324b86e1e1572f1112856f259486)


![{\displaystyle t_{0'}={\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55d4870d463087e6a448971e945eb96e96e5c5b0)

![{\displaystyle t_{0'}={\sqrt[{3}]{-8}}=-2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a55fb06f4a70ae3cdbbbca2d8ec340882b116f6b)




![{\displaystyle {\sqrt[{3}]{z}}={\sqrt[{3}]{|z|}}\cdot e^{\phi /3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e533e931781e8b08eb8defc5b1fb85a4fbe08e81)



![{\displaystyle f:z\to t:\ t={\sqrt[{3}]{z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3889a5d660b262a9e09e12c3e4128c77301aea68)
![{\displaystyle z={\begin{cases}|z|e^{i\phi }\\[3px]|z|e^{i(\phi +2\pi )}\\[3px]|z|e^{i(\phi -2\pi )}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a0aa804b8badf802fd7b03a1b01d1669529d336)
![{\displaystyle t={\sqrt[{3}]{z}}={\begin{cases}{\sqrt[{3}]{|z|}}e^{i\phi /3}\\{\sqrt[{3}]{|z|}}e^{i(\phi +2\pi )/3}\\{\sqrt[{3}]{|z|}}e^{i(\phi -2\pi )/3}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb522c05780e3b070774a8250670edd4fc3f04ba)









![{\displaystyle {\sqrt[{3}]{2}}=1.2599210498948732}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b1124e625ef5ea052e9812420d58d3335843bb7)










![{\displaystyle x_{i+1}={\tfrac {4}{3}}{\sqrt[{4}]{ax_{i}}}-{\tfrac {1}{3}}x_{i}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b71799039e60395897bd00bef7c191dd153b636f)
![{\displaystyle {\begin{aligned}{\sqrt[{3}]{1}}&=1&{\sqrt[{3}]{11}}\approx 2{,}2239800905693155211653633...\\{\sqrt[{3}]{2}}&\approx 1{,}2599210498948731647672106...&{\sqrt[{3}]{12}}\approx 2{,}2894284851066637356160844...\\{\sqrt[{3}]{3}}&\approx 1{,}4422495703074083823216383...&{\sqrt[{3}]{13}}\approx 2{,}3513346877207574895000163...\\{\sqrt[{3}]{4}}&\approx 1{,}5874010519681994747517056...&{\sqrt[{3}]{14}}\approx 2{,}4101422641752299861283696...\\{\sqrt[{3}]{5}}&\approx 1{,}7099759466766969893531088...&{\sqrt[{3}]{15}}\approx 2{,}4662120743304701014916113...\\{\sqrt[{3}]{6}}&\approx 1{,}8171205928321396588912117...&{\sqrt[{3}]{16}}\approx 2{,}5198420997897463295344212...\\{\sqrt[{3}]{7}}&\approx 1{,}9129311827723891011991168...&{\sqrt[{3}]{17}}\approx 2{,}5712815906582353554531872...\\{\sqrt[{3}]{8}}&=2&{\sqrt[{3}]{18}}\approx 2{,}6207413942088966071416612...\\{\sqrt[{3}]{9}}&\approx 2{,}0800838230519041145300568...&{\sqrt[{3}]{19}}\approx 2{,}6684016487219448673396273...\\{\sqrt[{3}]{10}}&\approx 2{,}1544346900318837217592935...&{\sqrt[{3}]{20}}\approx 2{,}7144176165949065715180894...\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/022dd02f9bd72b5773b16733ce205f2199b88b51)
















