Discriminante de um corpo de números algébricos

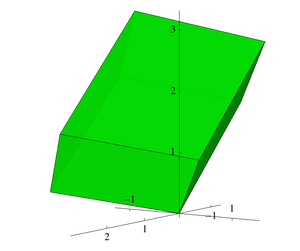
Em matemática, o discriminante de um corpo de números algébricos é um invariante numérico que, grosso modo, mede o tamanho do (anel de inteiros do) corpo. Mais especificamente, o discriminante é proporcional ao volume ao quadrado do domínio fundamental do anel de inteiros, e caracteriza quais primos se ramificam no corpo.

O discriminante é um dos invariantes mais básicos de um corpo de números e ocorre em várias fórmulas analíticas importantes, como a equação funcional da função zeta de Dedekind de K e a fórmula do número de classes para K. Um teorema de Hermite afirma que existe apenas um número finito de corpos de números com discriminante prescrito, no entanto, determinar essa quantidade precisamente ainda é um problema em aberto e o assunto da pesquisa atual.^[1]

O discriminante de K pode ser referido como o discriminante absoluto de K, para distinguí-lo da noção de discriminante relativo de uma extensão K/L de corpos de números. Este último é um ideal no anel de inteiros de L e, assim como o discriminante absoluto, indica quais primos de L são ramificados em K. Esta é uma generalização do discriminante absoluto, permitindo que L seja maior que Q; de fato, quando L = Q, o discriminante relativo de K/Q é o ideal principal de Z gerado pelo discriminante absoluto de K.

Seja K um corpo de números algébricos e seja O_K seu anel de inteiros. Seja b₁, ..., b_n uma base integral de O_K (ou seja, uma base como um Z-módulo), e seja {σ₁, ..., σ_n } o conjunto de mergulhos de K no números complexos (isto é homomorfismos de anel injetores K → C). O discriminante de K é o quadrado do determinante da matriz n-por-n B cuja entrada (i, j) é dada por σ_i(b_j). Simbolicamente,

${\displaystyle \Delta _{K}=\det \left({\begin{array}{cccc}\sigma _{1}(b_{1})&\sigma _{1}(b_{2})&\cdots &\sigma _{1}(b_{n})\\\sigma _{2}(b_{1})&\ddots &&\vdots \\\vdots &&\ddots &\vdots \\\sigma _{n}(b_{1})&\cdots &\cdots &\sigma _{n}(b_{n})\end{array}}\right)^{2}.}$

Equivalentemente, o traço de K para Q pode ser usado. Mais especificamente, defina a forma do traço como a matriz cuja entrada (i, j) dada por Tr_K/Q(b_ib_j). Essa matriz é igual a B^TB, e então o discriminante de K é o determinante dessa matriz.

• Corpos de números quadráticos: se d um inteiro livre de quadrados, então o discriminante de ${\displaystyle K=\mathbf {Q} ({\sqrt {d}})}$ é dado por^[2]

${\displaystyle \Delta _{K}=\left\{{\begin{array}{ll}d&{\text{if }}d\equiv 1{\pmod {4}}\\4d&{\text{if }}d\equiv 2,3{\pmod {4}}.\\\end{array}}\right.}$

Um inteiro que ocorre como discriminante de um corpo de números quadráticos é chamado de discriminante fundamental.^[3]

• Corpos ciclotômicos: sejam n > 2 um inteiro, ζ _n uma n-ésima raiz primitiva da unidade, e K_n = Q(ζ_n) o n-ésimo corpo ciclotômico. O discriminante de K_n é dado por^[2][4]

${\displaystyle \Delta _{K_{n}}=(-1)^{\varphi (n)/2}{\frac {n^{\varphi (n)}}{\displaystyle \prod _{p|n}p^{\varphi (n)/(p-1)}}}}$

Onde ${\displaystyle \varphi (n)}$ é a função totiente de Euler, e o produto no denominador percorre os primos p que dividem n.

• Base de potências: No caso em que o anel de inteiros tem uma base integral de potência, ou seja, pode ser escrito como O_K = Z[α], o discriminante de K é igual ao discriminante do polinômio mínimo de α. Para ver isso, pode-se escolher a base integral de O_K como sendo b₁ = 1, b₂ = α, b₃ = α², ..., b_n = αⁿ⁻¹. Assim, a matriz na definição é a matriz de Vandermonde associada a α_i = σ_i(α), cujo quadrado do determinante é igual a

${\displaystyle \prod _{1\leq i<j\leq n}(\alpha _{i}-\alpha _{j})^{2}}$,

exatamente a definição do discriminante do polinômio mínimo.

• Seja K = Q(α) o corpo de números obtido adjuntando uma raiz α do polinômio x ³ − x² − 2x − 8. Este foi o primeiro exemplo dado por Richard Dedekind de um corpo de números cujo anel de inteiros não possui uma base de potências. Uma base integral é dada por {1, α, α(α+1)/2} e o discriminante de K é − 503. ^{[5] [6]}
• Discriminantes repetidos: o discriminante de um corpo quadrático identifica-o exclusivamente, mas isso não é verdade em geral para corpos de números de grau maior. Por exemplo, existem dois corpos cúbicos não-isomorfos de discriminante 3969. Estes são obtidos adjuntando uma raiz dos polinômios x³ − 21x + 28 ou x³ − 21x − 35, respectivamente.^[7]

• Teorema de Brill : ^[8] O sinal do discriminante é dado por (−1)^r₂, onde r₂ é o número de pares de mergulhos complexos de K em C. ^[9]
• Um primo p ramifica em K se e somente se p divide Δ_K.^[10]
• Teorema de Stickelberger:^[11]

${\displaystyle \Delta _{K}\equiv 0{\text{ ou }}1{\pmod {4}}.}$

• Cota de Minkowski: ^[12] Seja n o grau da extensão K/Q e r₂ o número de pares de mergulhos complexos de K em C, então

${\displaystyle |\Delta _{K}|^{1/2}\geq {\frac {n^{n}}{n!}}\left({\frac {\pi }{4}}\right)^{r_{2}}\geq {\frac {n^{n}}{n!}}\left({\frac {\pi }{4}}\right)^{n/2}.}$

• Teorema de Minkowski: ^[13] Se K é diferente de Q, então |Δ_K| > 1 (segue diretamente da cota de Minkowski).
• Teorema de Hermite–Minkowski:^[14] Seja N um inteiro positivo. Existe apenas um número finito de corpos de números algébricos K (a menos de isomorfismo) com |Δ_K| < N. Novamente, isso segue da cota de Minkowski junto com o teorema de Hermite (de que existe apenas um número finito de corpos de números algébricos discriminante prescrito).

A definição original de discriminante de um corpo de números algébricos geral K foi dada por Dedekind em 1871.^[15] Nesse ponto, ele já conhecia a relação entre o discriminante e ramificação.^[16]

O teorema de Hermite antecede a definição geral do discriminante, com Charles Hermite publicando sua demonstração em 1857.^[17] Em 1877, Alexander von Brill determinou o sinal do discriminante.^[18] Leopold Kronecker enunciou pela primeira vez o teorema de Minkowski em 1882,^[19] embora a primeira demonstração tenha sido dada por Hermann Minkowski em 1891.^[20] No mesmo ano, Minkowski publicou seu limite sobre o discriminante.^[21] Perto do final do século XIX, Ludwig Stickelberger obteve seu teorema sobre o resíduo do módulo discriminante quatro.^[22][23]

O discriminante definido acima é algumas vezes referido como o discriminante absoluto de K para distingui-lo do discriminante relativo Δ_K/L de uma extensão de corpos de números K/L, que é um ideal em O_L. O discriminante relativo é definido de forma semelhante ao discriminante absoluto, mas deve-se levar em consideração que os ideais em O_L podem não ser principais e que pode não haver uma O_L-base de O_K. Seja {σ₁, ..., σ_n } o conjunto de mergulhos de K em C que são a identidade em L. Se b₁, ..., b_n é uma base qualquer de K sobre G, e seja d(b₁, ..., b_n) o quadrado do determinante da matriz N-por-N cuja entrada (i, j) é igual a σ_i(b_j). Então, o discriminante relativo de K/L é o ideal gerado pelos d(b₁, ...,b_n) conforme {b₁, ..., b_n} varia sobre todas as bases integrais de K/L (ou seja, bases com a propriedade que b_i ∈ O _K para todo i). Alternativamente, o discriminante relativo de K/L é a norma do diferente de K/L.^[24] Quando L = Q, o discriminante relativo Δ_K/Q é o ideal principal de Z gerado pelo discriminante absoluto Δ_K. Em uma torre de corpos K/L/F, os discriminantes relativos são relacionados por

${\displaystyle \Delta _{K/F}={\mathcal {N}}_{L/F}\left({\Delta _{K/L}}\right)\Delta _{L/F}^{[K:L]}}$

onde ${\displaystyle {\mathcal {N}}}$ denota norma relativa.^[25]

O discriminante relativo controla a ramificação da extensão de corpos K/L. Um ideal primo p de L se ramifica em K se, e somente se, este divide o discriminante relativo Δ_K/L. Uma extensão é não-ramificada se, e somente se, o discriminante for o ideal trivial.^[24] A cota de Minkowski acima mostra que não há extensões não-triviais não-ramificadas de Q. Os corpos maiores do que Q podem ter extensões não-ramificadas: por exemplo, para qualquer corpo com número de classes maior que um, seu corpo de classes de Hilbert é uma extensão não-trivial não-ramificada.

O discriminante-raiz de um corpo de números K de grau n é definido pela fórmula

${\displaystyle \operatorname {rd} _{K}=|\Delta _{K}|^{1/n}.}$^[26]

A relação entre discriminantes relativos em uma torre de corpos mostra que o discriminante-raiz não muda em uma extensão não-ramificada.

Dados números racionais não negativos ρ e σ, não ambos nulos, e um inteiro positivo n tal que o par (r, 2s) = (ρn, σn) está em Z×2Z, seja α_n(ρ, σ) o ínfimo de rd_K conforme K varia sobre corpos de números de grau n com r mergulhos reais e 2s mergulhos complexos, e seja α(ρ, σ) = liminf_n→∞ α_n(ρ, σ). Então

${\displaystyle \alpha (\rho ,\sigma )\geq 60.8^{\rho }22.3^{\sigma }}$ ,

e a hipótese de Riemann generalizada implica a cota mais forte

${\displaystyle \alpha (\rho ,\sigma )\geq 215.3^{\rho }44.7^{\sigma }.}$ ^[27]

Há também uma cota inferior que vale para todo grau, não apenas assintoticamente: para corpos totalmente reais, o discriminante-raiz é >14, com exatamente 1229 exceções.^[28]

Por outro lado, a existência de uma torre de corpos de classes infinita pode dar cotas superiores para os valores de α(ρ, σ). Por exemplo, a torre de corpos de classes infinita sobre Q (√-m) com m = 3·5·7·11·19 produz corpos de grau arbitrariamente grande com discriminante-raiz 2√m ≈ 296,276,^[27] e então α(0,1) < 296,276. Usando torres "tamely ramified", Hajir e Maire mostraram que α(1,0) < 954,3 e α(0,1) < 82,2,^[26] melhorando as cotas anteriores de Martinet.^[29]

• Quando mergulhado em ${\displaystyle K\otimes _{\mathbf {Q} }\mathbf {R} }$, o volume do domínio fundamental de O_K é ${\displaystyle {\sqrt {|\Delta _{K}|}}}$ (às vezes uma medida diferente é usada e o volume obtido é ${\displaystyle 2^{-r_{2}}{\sqrt {|\Delta _{K}|}}}$, onde r ₂ é o número de mergulhos complexos de K em C).
• Devido a aparecer como volume, o discriminante também aparece na equação funcional da função zeta de Dedekind de K e, portanto, na fórmula do número da classes e no teorema de Brauer–Siegel.
• O discriminante relativo de K/L é o condutor Artin da representação regular do grupo de Galois de K/L. Isso fornece uma relação com os condutores Artin dos caráteres do grupo de Galois de K/L, chamada de fórmula do condutor-discriminante.^[30]

Referências

• Milne, James S. (1998), Algebraic Number Theory, consultado em 20 de agosto de 2008 

• Brill, Alexander von (1877), «Ueber die Discriminante», Mathematische Annalen, 12 (1): 87–89, MR 1509928, doi:10.1007/BF01442468, consultado em 22 de agosto de 2009 
• Dedekind, Richard (1871), Vorlesungen über Zahlentheorie von P.G. Lejeune Dirichlet 2 ed. , Vieweg, consultado em 5 de agosto de 2009 
• Dedekind, Richard (1878), «Über den Zusammenhang zwischen der Theorie der Ideale und der Theorie der höheren Congruenzen», Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 23 (1), consultado em 20 de agosto de 2009 
• Hermite, Charles (1857), «Extrait d'une lettre de M. C. Hermite à M. Borchardt sur le nombre limité d'irrationalités auxquelles se réduisent les racines des équations à coefficients entiers complexes d'un degré et d'un discriminant donnés», Crelle's Journal, 1857 (53): 182–192, doi:10.1515/crll.1857.53.182, consultado em 20 de agosto de 2009 
• Kronecker, Leopold (1882), «Grundzüge einer arithmetischen Theorie der algebraischen Grössen», Crelle's Journal, 92: 1–122, consultado em 20 de agosto de 2009 
• Minkowski, Hermann (1891a), «Ueber die positiven quadratischen Formen und über kettenbruchähnliche Algorithmen», Crelle's Journal, 1891 (107): 278–297, doi:10.1515/crll.1891.107.278, consultado em 20 de agosto de 2009 
• Minkowski, Hermann (1891b), «Théorèmes d'arithmétiques», Comptes rendus de l'Académie des sciences, 112: 209–212 
• Stickelberger, Ludwig (1897), «Über eine neue Eigenschaft der Diskriminanten algebraischer Zahlkörper», Proceedings of the First International Congress of Mathematicians, Zürich, pp. 182–193 

• Bourbaki, Nicolas (1994). Elements of the history of mathematics. Traduzido por Meldrum, John. Berlin: Springer-Verlag. ISBN 978-3-540-64767-6.
• Cohen, Henri (1993), A Course in Computational Algebraic Number Theory, ISBN 978-3-540-55640-4, Graduate Texts in Mathematics, 138, Berlin, New York: Springer-Verlag, MR 1228206 
• Cohen, Henri; Diaz y Diaz, Francisco; Olivier, Michel (2002), «A Survey of Discriminant Counting», in: Fieker, Claus; Kohel, David R., Algorithmic Number Theory, Proceedings, 5th International Syposium, ANTS-V, University of Sydney, July 2002, ISBN 978-3-540-43863-2, Berlin: Springer-Verlag, ISSN 0302-9743, Lecture Notes in Computer Science, 2369, pp. 80–94, MR 2041075, doi:10.1007/3-540-45455-1_7 
• Fröhlich, Albrecht; Taylor, Martin (1993), Algebraic number theory, ISBN 978-0-521-43834-6, Cambridge Studies in Advanced Mathematics, 27, Cambridge University Press, MR 1215934 
• Koch, Helmut (1997), Algebraic Number Theory, ISBN 3-540-63003-1, Encycl. Math. Sci., 62 2nd printing of 1st ed. , Springer-Verlag 
• Narkiewicz, Władysław (2004), Elementary and analytic theory of algebraic numbers, ISBN 978-3-540-21902-6, Springer Monographs in Mathematics 3 ed. , Berlin: Springer-Verlag, MR 2078267 
• Neukirch, Jürgen (1999). Algebraic Number Theory. Grunlehren der mathematischen Wissenschaften. 322. Berlin: Springer-Verlag. ISBN 978-3-540-65399-8.
• Serre, Jean-Pierre (1967), «Local class field theory», in: Cassels, J. W. S.; Fröhlich, Albrecht, Algebraic Number Theory, Proceedings of an instructional conference at the University of Sussex, Brighton, 1965, ISBN 0-12-163251-2, London: Academic Press, MR 0220701 
• Voight, John (2008), «Enumeration of totally real number fields of bounded root discriminant», in: van der Poorten, Alfred J.; Stein, Andreas, Algorithmic number theory. Proceedings, 8th International Symposium, ANTS-VIII, Banff, Canada, May 2008, ISBN 978-3-540-79455-4, Lecture Notes in Computer Science, 5011, Berlin: Springer-Verlag, pp. 268–281, MR 2467853, arXiv:0802.0194, doi:10.1007/978-3-540-79456-1_18 
• Washington, Lawrence (1997), Introduction to Cyclotomic Fields, ISBN 978-0-387-94762-4, Graduate Texts in Mathematics, 83 2 nd ed. , Berlin, New York: Springer-Verlag, MR 1421575