Barbier teoremi

Geometride, Barbier teoremi, kesin şekli ne olursa olsun, sabit genişliğe sahip her eğrinin çevresinin, genişliğinin π katı olduğunu belirtir.^[1] Bu teorem, ilk olarak Joseph-Émile Barbier tarafından 1860'ta yayınlandı.^[2]

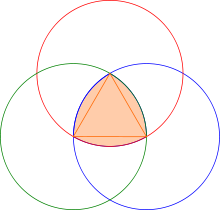
Sabit genişliğe sahip eğrilerin en bilinen örnekleri çember ve Reuleaux üçgenidir. Bir çember için genişlik, çapla aynıdır; ${\displaystyle w}$ genişliğinde bir çemberin çevresi ${\displaystyle \pi w}$'dur. ${\displaystyle w}$ genişliğine sahip bir Reuleaux üçgeni, ${\displaystyle w}$ yarıçaplı üç yaydan oluşur. Bu yayların her birinin merkezi açısı ${\displaystyle {\frac {\pi }{3}}}$ kadardır, bu nedenle ${\displaystyle w}$ genişliğindeki Reuleaux üçgenin çevresi, ${\displaystyle w}$ yarıçaplı bir dairenin çevresinin yarısına yani ${\displaystyle \pi w}$'ya eşittir. Reuleaux poligonları gibi diğer basit örneklerin benzer bir analizi de aynı sonucu verir.

Teoremin bir kanıtı, Minkowski toplamlarının özelliklerini kullanır. Eğer ${\displaystyle K}$, sabit ${\displaystyle w}$ genişliğine sahip bir cisim ise, ${\displaystyle K}$ ve 180° dönüşünün Minkowski toplamı yarıçapı ${\displaystyle w}$ ve çevresi ${\displaystyle 2\pi w}$ olan bir disktir. Bununla birlikte, Minkowski toplamı, dışbükey cisimlerin çevresi üzerinde doğrusal olarak etki eder, bu nedenle ${\displaystyle K}$'nin çevresi, teoremin belirttiği gibi ${\displaystyle \pi w}$ olan bu diskin çevresinin yarısı olmalıdır.^[3]

Alternatif olarak teorem, herhangi bir eğrinin uzunluğunun, eğriyi kesen çizgiler kümesinin ölçüsüne eşit olduğu ve bunların kesişme sayılarıyla çarpıldığı integral geometrideki Crofton formülünü takip eder. Aynı sabit genişliğe sahip herhangi iki eğri, aynı ölçüye sahip çizgi kümeleriyle kesişir ve bu nedenle aynı uzunluktadırlar. Tarihsel olarak, Crofton formülünü Barbier teoreminden daha sonra ve ondan bağımsız olarak türetmiştir.^[4]

Teoremin temel bir olasılık kanıtı, Buffon'un iğnesinde bulunabilir.

Barbier'in sabit genişliğe sahip yüzeyler için geliştirdiği teoreminin analojisi yanlıştır. Özellikle birim küre, ${\displaystyle 4\pi \approx 12,566}$ yüzey alanına sahipken, aynı sabit genişlikteki bir Reuleaux üçgeninin dönme yüzeyi ile ${\displaystyle 8\pi -{\tfrac {4}{3}}\pi ^{2}\approx 11,973}$ yüzey alanına sahiptir.^[5]

• Eric W. Weisstein, Barbier's Theorem (MathWorld)
• "Barbier teoremi". Encyclopedia of Mathematics. 4 Şubat 2015 tarihinde kaynağından arşivlendi. 
• Ross Honsberger (1970), "The Theorem of Barbier.", Ingenuity in Mathematics, Mathematical Association of America, ss. 157-64, doi:10.5948/UPO9780883859384.021 
• Fillmore, J. P. (1970), "Barbier's theorem in the Lobachevski plane", Proceedings of the American Mathematical Society, 24 (4), ss. 705-709, JSTOR 2037306 
• Cieslak, W., & Gozdz, S. (1990), "On Barbier's theorem", Matematički Vesnik, 42 (108), ss. 11-16 
• P. V. Araújo (1996), "Barbier's theorem for the sphere and the hyperbolic plane", Enseignment Mathematique, 2, 42 (3-4), ss. 295-309, Zbl 0937.53002 
• Bogomolny, A. (Eylül 2001), "The theorem of Barbier", MAA Online, 26 Ocak 2013 tarihinde kaynağından arşivlendi 
• Klamkin, M. S. (1955), "On Barbier's Solution of the Buffon Needle Problem", Mathematics Magazine, 28 (3), ss. 135-138, JSTOR 3029853 
• Yaz, N (2005), Sabit Genişlikli Eğrilerin Kinematiği (PDF), Ankara Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı, s. 14, Doktora Tezi 

• Blaschke–Lebesgue teoremi
• İzoperimetrik eşitsizlik
• Sabit genişlikteki eğrilerin alanlarını sınırlamak