Soma de Riemann

Na matemática, a soma de Riemann é uma aproximação obtida pela expressão ${\displaystyle \sum _{i=1}^{n}f(x_{i}^{*})\cdot \Delta x}$.

É nomeada em homenagem ao matemático alemão Bernhard Riemann. Uma aplicação muito comum é a aproximação da área de funções ou linhas em um gráfico, mas também o comprimento das curvas e outras aproximações.

A soma é dada pela divisão da região a ser calculada em formas (retângulos, trapézios, parábolas ou cubos) que juntos formam uma região que é similar àquela a ser medida, então calcula-se a área de cada uma das formas, e finalmente soma-se todas essas áreas menores juntas.  Essa abordagem pode ser usada para encontrar uma aproximação numérica para a integral definida mesmo se o teorema fundamental do cálculo não ajudar a encontrar uma forma fechada.

Tendo em vista que a região preenchida pelas formas menores geralmente não corresponde a exata forma da região a ser medida, a Soma de Riemann será diferente desta. Esse erro pode ser reduzido se a região for mais dividida, usando formas cada vez menores. Ao passo que as formas ficam menores, a soma se aproxima a Integral de Riemann.

Normalmente a Soma de Riemann tem uma aplicação ótima para funções polinomiais ou algébricas, o que significa que é possível precisar o valor exato do limite da soma com facilidade. Porém, para funções ditas transcendentes o cálculo da integral definida é não trivial por Riemann, ocorrendo ele comumente pela formação de retângulos de forma análoga ao método da exaustão.

Considere f:D → R sendo uma função definida do subconjunto D, de números reais, R. Tome I = [a, b] como um intervalo fechado contido em D, e

${\displaystyle P=[x_{0},x_{1}],[x_{1},x_{2}],...,[x_{n-1},x_{n}],}$

sendo uma partição de I, onde

${\displaystyle a=x_{0}<x_{1}<x_{2}<...<x_{n}=b.}$

Uma soma de Riemann de f sobre I com a partição P é definida como

${\displaystyle S=\sum _{i\mathop {=} 1}^{n}f(x_{i}^{*})(x_{i}-x_{i-1}),x_{i-1}\leq x_{i}^{*}\leq x_{i}.}$

Atenção no uso de “uma” ao invés de “a” em referência a soma de Riemann. Isso ocorre pelo fato que a escolha de ${\displaystyle x_{i}^{*}}$  no intervalo ${\displaystyle [x_{i-1},x_{i}]}$  é arbitrária, dado o fato que qualquer função f definida em um intervalo I e na partição fixada P, pode produzir uma soma de Riemann diferente em decorrência de qual ${\displaystyle x_{i}^{*}}$ foi escolhido, desde que ${\displaystyle x_{i-1}\leq x_{i}^{*}\leq x_{i}}$ se mantenha verdadeiro.

Exemplo: Escolhas específicas de ${\displaystyle x_{i}^{*}}$ nos dão diferentes tipos de soma de Riemann:

• Se ${\displaystyle x_{i}^{*}=x_{i-1}}$ para todo i, então S é chamado de Soma de Riemann à Esquerda;
• Se ${\displaystyle x_{i}^{*}=x_{i}}$ para todo i, então  S é chamado de Soma de Riemann à Direita;
• Se ${\displaystyle x_{i}^{*}={\frac {1}{2}}(x_{i}+x_{i-1})}$ para todo i, então é S é chamado de Soma de Riemann Média.
• A média entre a Soma à Esquerda e a Soma à Direita é chamada de Soma Trapezoidal.
• Se é dado que ${\displaystyle S=\sum _{i\mathop {=} 1}^{n}v_{i}(x_{i}-x_{i-1}),}$  onde ${\displaystyle v_{i}}$ é o supremo de f sobre ${\displaystyle [x_{i-1},x_{i}]}$ , então S é definido como uma Soma de Riemann Superior;
• De forma semelhante, se ${\displaystyle v_{i}}$ é o ínfimo de f sobre ${\displaystyle [x_{i-1},x_{i}]}$ , então S é definido como uma Soma de Riemann Inferior.

Qualquer soma de Riemann em dada partição (isto é, qualquer soma obtida pela escolha de ${\displaystyle x_{i}^{*}}$ entre ${\displaystyle x_{i-1}}$ e ${\displaystyle x_{i}}$ ) está entre as somas de Riemann superior e a inferior. Uma função é definida como integrável por Riemann se a soma inferior e superior forem se aproximando conforme a partição se afina. Este fato pode ser também usado para a integração numérica.

Os quatro métodos de Riemann para a soma são geralmente melhor usados com partições de tamanhos equivalentes. O intervalo [a, b] é, portanto, dividido em n subintervalos, de comprimento

${\displaystyle \Delta x={b-a \over n}.}$   Os pontos na partição serão então ${\displaystyle a,a+\Delta x,a+2\Delta x,...,a+(n-2)\Delta x,a+(n-1)\Delta x,b.}$

Para a Soma de Riemann à Esquerda, aproxima-se a função pelo seu valor no ponto final à esquerda, dando múltiplos retângulos com base Δx e altura f(a+iΔx). Tomando para i = 0, 1, ... n-1, e adicionando as áreas resultantes temos

${\displaystyle \Delta x{}[f(a)+f(a+\Delta x)+f(a+2\Delta x)+...+f(b-\Delta x)].}$

 A soma de Riemann à esquerda resulta em uma superestimação se f está monotonicamente decrescendo nesse intervalo, e em uma subestimação se f está monotonicamente crescendo.

Nessa soma, aproxima-se f de seu valor no ponto final à direita. São gerados, então, múltiplos retângulos de base Δx e altura f(a+Δx). Tomando para i – 1 , ..., n e adicionando as áreas resultantes se produz

${\displaystyle \Delta x{}[f(a+\Delta x)+f(a+2\Delta x)+...+f(b)].}$  

A soma de Riemann à direita resulta em uma subestimação se f está monotonicamente decrescendo, e uma superestimação se f está

monotonicamente crescendo. O erro na fórmula será

${\displaystyle \left|\int _{a}^{b}f(x)dx-A_{direita}\right|\leq {\frac {M_{1}(b-a)^{2}}{2n}},}$

 onde ${\displaystyle M_{1}}$ é o valor máximo do valor absoluto de ${\displaystyle f'(x)}$ nesse intervalo.

Aproximando f no ponto médio dos intervalos expressam f(a+Δx/2) para o primeiro intervalo, para o próximo temos f(a+3Δx/2), e assim por diante até f(b-Δx/2). Somando as áreas temos

${\displaystyle \Delta x[f(a+{\frac {\Delta x}{2}})+f(a+{\frac {3\Delta x}{2}})+...+f(b-{\frac {\Delta x}{2}})].}$ 

O erro dessa formula será

${\displaystyle \left|\int _{a}^{b}f(x)dx-A_{media}\right|\leq {\frac {M_{2}(b-a)^{3}}{24n^{2}}},}$

onde ${\displaystyle M_{2}}$ é o valor máximo do valor absoluto de ${\displaystyle f''(x)}$ nesse intervalo.

Nesse caso, os valores da função f no intervalo são aproximados pela média dos valores nos pontos finais da direita e da esquerda. Dessa mesma maneira, um simples cálculo usando a formula da área

${\displaystyle A={\frac {1}{2}}h(b_{1}+b_{2})}$

 para um trapézio de lados paralelos b₁, b₂ e altura h produz

${\displaystyle {\frac {1}{2}}\Delta x[f(a)+2f(a+\Delta x)+2f(a+2\Delta x)+2f(a+3\Delta x)+...+2f(b-\Delta x)+f(b)].}$

O erro dessa fórmula será

${\displaystyle \left|\int _{a}^{b}f(x)dx-A_{trap}\right|\leq {\frac {M_{2}(b-a)^{3}}{12n^{2}}},}$

 onde ${\displaystyle M_{2}}$ é o valor máximo do valor absoluto de ${\displaystyle f''(x).}$

 A aproximação obtida com a regra do trapézio para a função é o mesmo que a média da somas esquerdas e direitas dessa função.

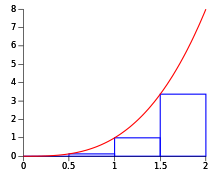
Tomado um exemplo, a área sob a curva de y=x² entre 0 e 2 pode ser processualmente computada usando o método de Riemann.

O intervalo [0,2] é primeiramente dividido em n subintervalos, cada um deles com comprimento de ${\displaystyle {\frac {2}{n}}}$ ; esse é o comprimento dos retângulos de Riemann (a seguir chamadas “caixas”). Já que será usada a soma de Riemann à direita, a sequência de coordenadas x para as caixas será ${\displaystyle x_{1},x_{2},...,x_{n}}$. Dessa forma, a sequência de alturas das caixas será ${\displaystyle x_{1}^{2},x_{2}^{2},...,x_{n}^{2}}$. É um fato importante que ${\displaystyle x_{i}={\frac {2i}{n}}}$ e ${\displaystyle x_{n}=2}$.

A área de cada caixa será ${\displaystyle {\frac {2}{n}}\times x_{i}^{2}}$ e sendo assim a soma de Riemann à direita será: 

${\displaystyle {\begin{matrix}S&=&{\frac {2}{n}}\times \left({\frac {2}{n}}\right)^{2}+...+{\frac {2}{n}}\times \left({\frac {2i}{n}}\right)^{2}+...+{\frac {2}{n}}\times \left({\frac {2n}{n}}\right)^{2}\\&=&{\frac {8}{n^{3}}}(1+...+i^{2}+...n^{2})\\&=&{\frac {8}{n^{3}}}\left({\frac {n(n+1)(2n+1)}{6}}\right)\\&=&{\frac {8}{n^{3}}}\left({\frac {2n^{3}+3n^{2}+n}{6}}\right)\\&=&{\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}\end{matrix}}}$

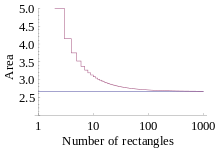
Se o limite é visualizado como  n → ∞, pode-se concluir que a aproximação alcança o valor real da área  sob a curva ao passo que o número de caixas aumenta.

Consequentemente:

${\displaystyle \lim _{n\to \infty }S=\lim _{n\to \infty }\left({\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}\right)={\frac {8}{3}}}$ .

Esse método concorda com a integral definida tal qual calculada nos modos mais mecânicos:

${\displaystyle \int _{0}^{2}x^{2}dx={\frac {8}{3}}}$

Integral de Riemann

Integral de Riemann-Stieltjes

Integral de Lebesgue

Fórmula de Simpson

Primitiva

• Thomas, George B. Jr.; Finney, Ross L. (1996), Calculus and Analytic Geometry (9th ed.), Addison Wesley, ISBN 0-201-53174-7