Relatividade restrita
| Relatividade especial |
|---|
 |
|
| Fundações
|
| Consequências
|
|
|
|
|
A Teoria da Relatividade Restrita ou Teoria da Relatividade Especial (abreviadamente TRR ou TRE), publicada pela primeira vez por Albert Einstein em 1905, descreve a física do movimento na ausência de campos gravitacionais.[1]
Até aquela época, pensava-se que o movimento de um corpo poderia ser descrito pela mecânica clássica para qualquer observador em um referencial inercial. Além disso, o movimento poderia ser descrito em um outro referencial com velocidade constante em relação ao referencial original por meio das transformações de Galileu. Sendo assim, todo referencial inercial seria equivalente. No entanto, a teoria do eletromagnetismo não obedece esses princípios, o que acabou levando à formulação das transformações de Lorentz por H. A. Lorentz.[2][3]
Dessas transformações e de contribuições de outros pesquisadores, como Henri Poincaré, Hermann Minkowski (posteriormente) e outros, Einstein formulou sua teoria da relatividade, introduzindo de forma definitiva conceitos como espaço-tempo, dilatação temporal, invariância da velocidade da luz, equivalência massa-energia e outros.[3]
História
Os fundamentos da relatividade restrita estão nas equações de Maxwell e na mecânica newtoniana, duas das grandes teorias da física que pareciam não conversar entre si.
As leis de Newton, que regem a mecânica clássica, foram feitas baseadas no princípio da relatividade de Galileu. Como consequência disso, as equações de movimento de um corpo obtidas em um referencial poderiam ser passadas para outro por meio das transformações de Galileu. Em outras palavras, as leis da Física são invariantes perante mudanças de referenciais. No entanto, foi percebido que os fenômenos eletromagnéticos não respeitam esses princípios. [4]
Quando James C. Maxwell publicou seu trabalho final unificando a eletricidade com o magnetismo, uma das grandes conclusões foi a determinação da velocidade de propagação das ondas eletromagnéticas no vácuo. Maxwell percebeu que o valor encontrado por ele coincidia com o valor medido experimentalmente para a velocidade da luz, concluindo que a luz era uma onda eletromagnética. A surpresa, porém, estava no fato de que a velocidade dessas ondas no vácuo é constante e, portanto, deveria ser a mesma para todo referencial inercial. Surge o conflito entre a mecânica clássica e o eletromagnetismo: as ondas eletromagnéticas parecem não seguir as transformações de Galileu.[2][5][6]
Dentre as alternativas para explicar, estava a hipótese do éter luminífero, uma substância estacionária que preencheria todo o espaço pela qual as ondas eletromagnéticos propagariam. Assim, o valor encontrado por Maxwell seria a velocidade da luz em relação ao éter. As transformações de Galileu seriam válidas, por exemplo, ao considerar-se o movimento da Terra em relação ao éter na hora de mudar o referencial da luz.[6] Várias foram a tentativa de medir a velocidade da Terra relativa ao éter, com o experimento de Michelson-Morley sendo a primeira forte evidência contra o éter, que até então predominava o meio acadêmico.[6] [7]
Diante dessa grande frustração, os físicos tentaram resolver a falta de observação do movimento da Terra em relação ao éter. Um dos pesquisadores mais proeminentes foi Hendrik Lorentz, que elaborou a hipótese de que a matéria sofreria uma contração no seu comprimento ao locomover-se no éter, conceito que viria a ser conhecido como contração de Lorentz. Essa ideia o levou a formular as transformações de Lorentz, uma série de transformações de coordenadas a fim adequar as transformações de Galileu para essa suposta interação com o éter.[2][5][6]
Finalmente, Einstein tentou resolver esse problema partindo de duas ideias, conhecidas hoje como postulados da relatividade especial:[3]
- As leis da Física são as mesmas para todos os referenciais inerciais, sendo, portanto, invariantes perante transformações de coordenadas.
- A velocidade da luz no vácuo é constante para todos os referenciais inerciais independente da velocidade da fonte emissora.
Partindo desses conceitos, Einstein conseguiu recuperar as transformações de Lorentz. Apesar disso, elas possuem um significado diferente nesse contexto. Para Lorentz, a contração ocorria devido à velocidade relativa do objeto ao éter, e como o éter era considerado como estando em repouso, qualquer outro referencial inercial observaria o objeto também contraído. Já para Einstein, a contração ocorria devido à velocidade do objeto em relação a determinado referencial, assim, para um referencial em repouso em relação ao objeto, seu comprimento continuaria o mesmo.[2]
Nascia, então, a teoria da relatividade especial. Consequências dessa nova teoria são a dilatação temporal, relatividade da simultaneidade, equivalência massa-energia, espaço-tempo, entre outros. Posteriormente, a incompatibilidade entre a Lei da Gravitação Universal de Isaac Newton e a relatividade restrita daria, em 1915, origem à Teoria da Relatividade Geral.
Os postulados da Relatividade Restrita
Princípio da relatividade
 Ver artigo principal: princípio da relatividade
Ver artigo principal: princípio da relatividadeUm dos conceitos mais básicos e fundamentais para a compreensão da teoria da relatividade são os sistemas de referências. De forma resumida, um referencial ou sistema de referência é um objeto matemático usado para realizar medidas físicas, como posição ou velocidade por exemplo. Sendo assim, é essencial que, ao estudarmos algum fenômeno, escolhamos um sistema de referência para fazermos as medições.
Escolhido um referencial, podemos registrar nele um evento. Neste contexto, evento significa qualquer acontecimento ao qual possa ser atribuído um único instante de tempo e ponto no espaço relativo ao sistema escolhido. Assim, podemos interpretar um evento como sendo um ponto no espaço-tempo. Por exemplo, podemos considerar a partida de um trem como um evento, já que podemos especificar o local em que isso ocorreu e o instante de tempo.[2][8][9]
Outra característica importante que o referencial deve ter é ser inercial. Brevemente, um referencial é dito inercial quando um objeto sob a ação de uma força resultante nula possui velocidade constante (nula ou não). Desse modo, se você tiver as coordenadas de um evento em certo referencial, ele pode ser descrito em um outro fazendo uma transformação de coordenadas. Disso, temos o princípio da relatividade: todas as leis da física devem ser válidas para todo e qualquer referencial inercial.[2][3][5][9]

Para melhor compreensão, segue um pequeno exemplo das transformações de Galileu:
Considere um referencial descrito pelas coordenadas , e um outro referencial descrito pelas coordenadas que se move com velocidade para a direita em relação a (esquema ilustrado na Figura 2).
Agora, suponha que há um objeto em repouso em relação a com coordenadas . Do ponto de pista de um observador em , este objeto estará se movendo para a esquerda com velocidade . Assim, suas coordenadas em para um dado instante de tempo será .[5]
Invariância da velocidade da luz
 Ver artigo principal: transformações de Lorentz
Ver artigo principal: transformações de LorentzAlém de supor a validade do princípio da relatividade, Einstein também supôs que a velocidade da luz, denotada por , deve ser invariante perante transformações de coordenadas. No entanto, esse postulado não respeita as transformações de Galileu. Sendo assim, conclui-se que é necessário ter um novo conjunto de relações entre sistemas de referência inerciais.
Há vários caminhos para se chegar a essas relações, alguns com argumentos puramente matemáticos, outros com argumentos originados de princípios físicos. Em um de seus livros[2], Einstein demonstra essas relações partindo de alguns simples argumentos físicos:[9]
- O espaço-tempo deve ser o mesmo em todo lugar, o que possibilita colocar a origem do sistema de referência em qualquer ponto.
- As transformações devem ser simétricas, isto é, você deve conseguir sair de um referencial para outro e, invertendo o sinal da velocidade entre eles, retornar ao original.
- Por fim, a velocidade da luz deve ser a mesma em ambos os referenciais.
Partindo disso e com um pouco de matemática, é possível chegar nas seguintes relações, chamadas transformações de Lorentz:
em que é o fator de Lorentz, e é a velocidade relativa entre os dois referenciais inerciais.
As relações acima nos possibilitam encontrar as coordenadas no referencial a partir das coordenadas no referencial . Mas, como as transformações são simétricas, para obtermos a partir de basta usarmos
Esses resultados levam às mesmas conclusões da hipótese do éter de Lorentz. A diferença, porém, está no fato de que o raciocínio desenvolvido por Einstein não requer que exista uma substância que permeia todo o espaço e, portanto, nega a existência de um referencial absoluto.[2] Assim, pelo princípio da navalha de Ockham (além de concordar com os experimentos que apontavam para a não existência do éter), a teoria da Relatividade Restrita foi preferível à hipótese do éter de Lorentz.
Apesar de supor A não existência de um referencial específico que seja absoluto, a Relatividade Restrita é válida somente para um conjunto específico de referenciais: os referenciais inerciais. Uma generalização que inclua também os referenciais não-inerciais viria apenas em 1915 com a teoria da Relatividade Geral.
Com esses dois postulados, torna-se possível desenvolver a teoria da relatividade restrita propriamente, culminando em uma série de consequências e resultados de grande relevância para a Física.
Consequências
Contração espacial
Dilatação temporal
Relatividade da simultaneidade
Equivalência entre massa e energia
 Ver artigo principal: Equivalência massa–energia
Ver artigo principal: Equivalência massa–energiaPode ser, no entanto, muito mais importante a demostração de que a energia e massa, antes consideradas propriedades mensuráveis diferenciadas, relacionavam-se através da que é, sem dúvida, a equação mais famosa de toda a física moderna:
,
onde E é a energia, m é a massa e c é a velocidade da luz no vácuo. Se o corpo está a se mover à velocidade v relativa ao observador, a energia total do corpo é:
- , onde
O γ surge em relatividade na derivação das transformações de Lorentz.
Quando v é muito menor que c pode-se usar uma aproximação de γ (obtida pelo desenvolvimento em série de Taylor),
igual à energia em repouso, mc², mais a energia cinética newtoniana, ½mv². Este é um exemplo de como as duas teorias coincidem quando as velocidades são pequenas.
Além do mais, à velocidade da luz, a energia será infinita, o que impede que as partículas que têm massa em repouso possam alcançar a velocidade da luz.
A implicação mais radical da teoria é que põe um limite superior às leis (ver Leis da natureza) da Mecânica clássica e gravidade propostas por Isaac Newton quando as velocidades se aproximam da velocidade da luz no vácuo. Nada que possa transportar massa ou informação pode mover-se tão ou mais rápido que a luz. Quando um objeto se aproxima da velocidade da luz (em qualquer sistema) a quantidade de energia diferencial requerida para a aumentar a sua velocidade aumenta de forma rápida e assimptótica até ao infinito, tornando impossível alcançar a velocidade da luz. Só partículas sem massa, como os fotões, podem alcançar a dita velocidade (além disso, devem mover-se em qualquer sistema de referência a essa velocidade) que é aproximadamente 300 000 quilómetros por segundo (3·108 ms−1).
O nome táquion foi usado para nomear partículas hipotéticas que se deslocariam sempre a uma velocidade superior à da luz. Atualmente ainda não há evidência experimental da sua existência.
A relatividade especial também afirma que o conceito de simultaneidade é relativo ao observador: se a matéria pode viajar ao longo de uma linha (trajetória) no espaço-tempo cuja velocidade em todo momento é menor que a da luz, a teoria chama a esta linha intervalo temporal. De forma semelhante, um intervalo espacial significa uma linha no espaço-tempo ao longo da qual nem a luz nem outro sinal mais lento poderiam viajar. Acontecimentos ao longo de um intervalo espacial não podem influenciar-se um ao outro transmitindo luz ou matéria, e podem aparecer como simultâneos a um observador num sistema de referência adequado. Para observadores em diferentes sistemas de referência, o acontecimento A pode parecer anterior a B ou vice-versa. Isto não sucede quando consideramos acontecimentos separados por intervalos temporais.
A Relatividade restrita é quase universalmente aceita pela comunidade física na atualidade, ao contrário da Relatividade Geral que, apesar de ter sido confirmada, foi-o com experiências que não invalidam algumas teorias alternativas da gravitação. Efetivamente, há ainda quem se opõe à TRR em vários campos, tendo sido propostas várias alternativas, como as chamadas Teorias do Éter.
Efeito Doppler relativístico
A Teoria
A TRR usa tensores ou quadrivectores para definir um espaço não-euclidiano (pseudo-euclidiano). Este espaço, na realidade, é semelhante em muitos aspectos, sendo fácil de trabalhar. O diferencial da distância (ds) num espaço euclidiano é definida como:
- ,
onde dx1, dx2, dx3 são diferenciais das três dimensões espaciais. Na geometria da relatividade especial, uma quarta dimensão, o tempo, foi acrescentada, mas é tratada como uma quantidade imaginária com unidades de tempo, ficando a equação para a distância, em forma diferencial, como:
- .
Essa expressão é conhecida como métrica de Minkowski. O seu significado físico é que exceto para visto mais adiante, sempre existe:
1) Ou um sistema de referência tal que e portanto é simplesmente uma distância entre pontos do espaço.
2) Ou um sistema de referência tal que e é um intervalo de tempo entre 2 eventos no mesmo lugar.
Considerando velocidade constante, esse último caso é fácil de entender. Um evento na Terra e outro um dia depois em Marte. No referencial de uma nave que chegasse em Marte em 1 dia, esses eventos aconteceriam no mesmo lugar.
Já se em vez de Marte alterarmos o segundo ponto para Alfa-Centauri, não é possível chegar lá em um dia, pois a velocidade seria maior que a da luz. Mas, para uma nave com uma dada velocidade, os 2 eventos seriam simultâneos, e portanto com .[9]
Se reduzirmos as dimensões espaciais para duas, podemos fazer uma representação física num espaço tridimensional,
- .
Podemos ver que as geodésicas com medida nula formam um cone duplo (cone de luz),

definido pela equação
ou
- .
A equação anterior é igual à equação do círculo com r = c dt. Se generalizarmos o anteriormente exposto às três dimensões espaciais, as geodésicas nulas tornam-se esferas concêntricas, com raio = distância = c*(+ ou -)tempo.
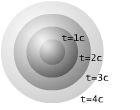
ou
- .
Este cone duplo de distâncias nulas representa o "horizonte de visão" de um ponto no espaço. Isto é, quando, ao olharmos uma estrela da qual dizemos "A estrela da qual estou a receber luz tem X anos", estamos a vê-la através dessa linha de visão: uma geodésica de distância nula. Estamos a ver um acontecimento que se deu a metros, e d/c segundos no passado. Por esta razão, o duplo cone é também conhecido como cone de luz. (O ponto inferior da esquerda do diagrama representa a estrela, a origem representa o observador e a linha representa a geodésica nula, o "horizonte de visão" ou cone de luz.)
Geometricamente O cone, na região -t inclui eventos que podem influenciar a origem (presente), enquanto que a região +t do cone engloba eventos que podem ser influenciados pela origem (presente). Desta forma, o que podemos ver é um espaço de horizontes. Eventos fora do cone de luz não podem segundo esta teoria influenciar o evento representado pelo vértice do cone.
Lei da conservação da energia cinética

No entanto, a geometria não se mantém constante quando existe aceleração, isto é, se . De fato, isto envolveria uma aplicação de força, e, por consequência, uma mudança na energia. A métrica para um referencial acelerado se altera, embora ainda num espaço-tempo plano. Já quando há presença de gravidade, precisamos da relatividade geral, em que a curvatura intrínseca do espaço-tempo é diretamente proporcional à densidade de energia no ponto referido.
Confirmação experimental da teoria da relatividade restrita
Ver:
- Experiência de Michelson-Morley – deriva do éter.
- Experiência de Hamar – obstrução do fluxo de éter.
- Experiência de Trouton-Noble - momento de torção num capacitor .
- Experiência de Kennedy-Thorndike – contracção do tempo.
- Experiência de Sagnac - variação de velocidade em sistema de espelhos rotativo.
- Experiência de Kaufman - deflexão de feixe de elétrons em concordância perfeita com a previsão de Lorentz-Einstein.
- Experiência de Rossi-Hall - medida da mudança da meia-vida característica de uma partícula no referencial do laboratório em função da velocidade.
- Experiência de Ives-Stilwell - mediu o desvio Doppler de luz emitida por raios canais do hidrogênio em sentidos opostos.
Tradução
- Albert Einstein (31 de julho de 2020). Traduzido por Oliver Fabio Piattella. «O artigo fundador da teoria da relatividade restrita: Sobre a eletrodinâmica dos corpos em movimento». Cadernos de Astronomia (1): 157–176. ISSN 2675-4754. doi:10.47083/Cad.Astro.v1n1.31681
Referências
- ↑ Greene, B. (2001). O Universo Elegante 🔗. [S.l.]: Companhia das Letras. ISBN 978-8535900989
- ↑ a b c d e f g h Einstein, A. (2022). A teoria da relatividade: Sobre a teoria da relatividade especial e geral. [S.l.]: L&PM Editores. ISBN 978-6556663272
- ↑ a b c d Lorentz, H.; Einstein, A.; Minkowski, H.; Weyl, H.; Sommerfeld, A. (1952). The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity. [S.l.]: Dover Publications. ISBN 978-0486600819
- ↑ Goldstein, H.; Poole, C.; Safko, J. (2002). Classical Mechanics. [S.l.]: Addison Wesley. ISBN 978-0201657029
- ↑ a b c d Einstein, A. (1921). «A Brief Outline of the Development of the Theory of Relativity». Nature. 106 (2677): 782-784. doi:10.1038/106782a0
- ↑ a b c d Ferraro, R. (2014). «From Æther Theory to Special Relativity». In: Ashtekar, A.; Petkov, V. Springer Handbook of Spacetime. [S.l.]: Springer. pp. 3–25. ISBN 978-3642419928
- ↑ Michelson, A.; Morley, E. (1887). «On the relative motion of the Earth and the luminiferous ether». American Journal of Science. s3-34 (203): 333-345. doi:10.2475/ajs.s3-34.203.333
- ↑ Taylor, E.; Wheeler, J. (1992). Spacetime Physics. [S.l.]: W. H. Freeman. ISBN 978-0716723271
- ↑ a b c d Susskind, L.; Friedman, A. (2017). Special Relativity and Classical Field Theory. [S.l.]: Penguin UK. ISBN 978-0241293362
Ligações externas
- «Special relativity» (em inglês)
- «What is the experimental basis of Special Relativity?» (em inglês)
 Portal da física
Portal da física Portal da ciência
Portal da ciência














































