Równanie pędu Cauchy’ego

Równanie pędu Cauchy’ego – wektorowe równanie różniczkowe cząstkowe zaproponowane przez Cauchy’ego, które opisuje nierelatywistyczny transport pędu w każdym ośrodku ciągłym^[1]. Dane jest ono następująco:

${\displaystyle \rho {\frac {d{\vec {v}}}{dt}}=\nabla \cdot {\boldsymbol {\sigma }}+\rho {\vec {f}}}$

gdzie:

${\displaystyle \rho \;\mathrm {[kg/m^{3}]} }$ – gęstość,

${\displaystyle d{\vec {v}}/dt=\partial _{t}{\vec {v}}+{\vec {v}}\cdot \nabla {\vec {v}}\;\mathrm {[m/s^{2}]} }$ – pochodna substancjalna prędkości,

${\displaystyle \nabla \;\mathrm {[1/m]} }$ – operator nabla,

${\displaystyle {\boldsymbol {\sigma }}\;\mathrm {[Pa=N/m^{2}]} }$ – tensor naprężenia,

${\displaystyle {\vec {f}}\;\mathrm {[m/s^{2}]} }$ – przyspieszenie związane z siłami masowymi.

Jest to równanie wektorowe (tzn. jego rozwiązaniem jest pole wektorowe) które po rozwinięciu w układzie kartezjańskim ma postać trzech równań – po jednym dla każdej składowej wynikowego pola wektorowego^[2]:

${\displaystyle {\begin{aligned}x&:&\rho \left({\frac {\partial u}{\partial t}}+u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}+w{\frac {\partial u}{\partial z}}\right)&={\frac {\partial \sigma _{xx}}{\partial x}}+{\frac {\partial \sigma _{yx}}{\partial y}}+{\frac {\partial \sigma _{zx}}{\partial z}}+\rho f_{x}\\[8pt]y&:&\rho \left({\frac {\partial v}{\partial t}}+u{\frac {\partial v}{\partial x}}+v{\frac {\partial v}{\partial y}}+w{\frac {\partial v}{\partial z}}\right)&={\frac {\partial \sigma _{xy}}{\partial x}}+{\frac {\partial \sigma _{yy}}{\partial y}}+{\frac {\partial \sigma _{zy}}{\partial z}}+\rho f_{y}\\[8pt]z&:&\rho \left({\frac {\partial w}{\partial t}}+u{\frac {\partial w}{\partial x}}+v{\frac {\partial w}{\partial y}}+w{\frac {\partial w}{\partial z}}\right)&={\frac {\partial \sigma _{xz}}{\partial x}}+{\frac {\partial \sigma _{yz}}{\partial y}}+{\frac {\partial \sigma _{zz}}{\partial z}}+\rho f_{z}\end{aligned}}}$

Jak widać układ nie jest zamknięty, gdyż mamy tylko 3 równania a 13 niewiadomych tj. ${\displaystyle \rho }$ (skalar – 1 niewiadoma), ${\displaystyle {\vec {v}}}$ (vektor – 3 niewiadome), ${\displaystyle {\boldsymbol {\sigma }}}$ (macierz – 9 niewiadomych). Poza tym ${\displaystyle t,x,y,z,{\vec {f}}}$ są wiadome w ramach warunków początkowych/brzegowych.

Detale dotyczące ${\displaystyle \nabla \cdot {\boldsymbol {\sigma }}}$

Dla ${\displaystyle \nabla \cdot {\boldsymbol {\sigma }}}$ operacja „${\displaystyle \cdot }$” pomiędzy operatorem nabla ${\displaystyle \nabla }$ a tensorem naprężenia ${\displaystyle {\boldsymbol {\sigma }}}$ NIE JEST mnożeniem macierzy – nie można użyć lewostronnego mnożenia pomiędzy wektorem kontrawariantnym (kolumnowym; „pionowym”; co wynika z definicji operatora) a macierzą. Wyrażenie ${\displaystyle \nabla \cdot {\boldsymbol {\sigma }}}$ ma tylko symboliczne znaczenie. Standardowo dywergencja jest zdefiniowana jako operator na polu wektorowym (jako Iloczyn skalarny pomiędzy operatorem nabla i wektorem (więcej: Pochodna kowariantna)), ale może zostać rozszerzona na pola tensorowe 2 rzędu (macierze), jednak w tym przypadku mamy do czynienia z inną operacją: ${\displaystyle \nabla \cdot {\boldsymbol {\sigma }}={\cfrac {\partial \sigma _{ki}}{\partial x_{k}}}~\mathbf {e} _{i}=\sigma _{ki,k}~\mathbf {e} _{i}}$. W ogólności mamy ${\displaystyle \nabla \cdot {\boldsymbol {\sigma }}\neq \mathrm {div} ({\boldsymbol {\sigma }})=\nabla \cdot {\boldsymbol {\sigma }}^{T}.}$ W kartezjańskim układzie współrzędnych możemy tę operację zapisać jako mnożenie macierzy (poniżej używamy „pusty” symbol mnożenia) w następujący sposób: ${\displaystyle \nabla \cdot {\boldsymbol {\sigma }}=(\nabla ^{T}{\boldsymbol {\sigma }})^{T}=\left({\begin{bmatrix}{\frac {\partial }{\partial x}}\\{\frac {\partial }{\partial y}}\\{\frac {\partial }{\partial z}}\end{bmatrix}}^{T}{\begin{bmatrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\end{bmatrix}}\right)^{T}=\left(\left[{\tfrac {\partial }{\partial x}}\ \ {\tfrac {\partial }{\partial y}}\ \ {\tfrac {\partial }{\partial z}}\right]{\begin{bmatrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\end{bmatrix}}\right)^{T}={\begin{bmatrix}{\frac {\partial \sigma _{xx}}{\partial x}}+{\frac {\partial \sigma _{yx}}{\partial y}}+{\frac {\partial \sigma _{zx}}{\partial z}}\\{\frac {\partial \sigma _{xy}}{\partial x}}+{\frac {\partial \sigma _{yy}}{\partial y}}+{\frac {\partial \sigma _{zy}}{\partial z}}\\{\frac {\partial \sigma _{xz}}{\partial x}}+{\frac {\partial \sigma _{yz}}{\partial y}}+{\frac {\partial \sigma _{zz}}{\partial z}}\end{bmatrix}}}$ gdzie rezultat (po prawej) jest kolumnowym wektorem, ${\displaystyle \mathbb {\ } ^{T}}$ oznacza transpozycję. Transpozycja operatora nabla w powyższych równaniach pozwala na użycie lewostronnego mnożenia macierzy (od drugiej równości), kolejna transpozycja (wykonana po mnożeniu macierzowym) zmienia rezultat z wektora wierszowego na kolumnowy (kontrawariantnym) co powzowli na dodawanie pozostałych składowych równania pędu (które są wektorami kolumnowymi) jak np. ${\displaystyle \rho {\vec {f}}.}$ Dla przypadku gdy sigma jest tensorem symetrycznym ${\displaystyle \sigma _{ij}=\sigma _{ji}}$ (np. dla płynu Newtonowskiego w równaniach Naviera-Stokesa bazujących na równaniu pędu Cauchego) zachodzi ${\displaystyle \nabla \cdot {\boldsymbol {\sigma }}=\mathrm {div} ({\boldsymbol {\sigma }}).}$ Jednak w ogólności nie powinniśmy mylić operacji ${\displaystyle \nabla \cdot {\boldsymbol {\sigma }}}$ z operacją ${\displaystyle \mathrm {div} ({\boldsymbol {\sigma }})}$ która dla niesymetrycznego tensora sigma (używanym np. dla modelowania płynów nienewtonowskich jak polimery) daje inne rezultaty[3]

Wychodzimy od uogólnionej zasady zachowania pędu, którą można zapisać następująco: „zmiana pędu układu jest proporcjonalna do siły wypadkowej działającej na ten układ” wyraża się ona wzorem:

${\displaystyle {\vec {p}}(t+\Delta t)-{\vec {p}}(t)=\Delta t{\vec {\bar {F}}}}$

gdzie:

${\displaystyle {\vec {p}}(t)}$ – pęd w chwili ${\displaystyle t,}$

${\displaystyle {\vec {\bar {F}}}}$ – uśredniona w czasie ${\displaystyle \Delta t}$ siła.

Po podzieleniu przez ${\displaystyle \Delta t}$ i przejściu do granicy ${\displaystyle \Delta t\to 0}$ otrzymujemy:

${\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}}}$

Skupimy się teraz kolejno na wyznaczeniu lewej, a następnie prawej strony powyższego równania dla stałej masy w różniczkowej sześciennej objętości kontrolnej (czyli elemencie ciała) której pęd i działające nań siły chcemy zbadać. Na koniec zestawimy lewą i prawą stronę powyższego równania, otrzymując równanie Pędu Cauchy’ego.

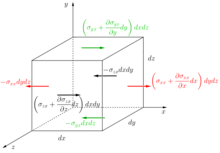
Siły dzielimy na masowe i powierzchniowe

${\displaystyle {\vec {F}}={\vec {F}}_{p}+{\vec {F}}_{m}}$

Na ścianki objętości kontrolnej działają siły powierzchniowe. Składowa X tych sił (w formie iloczynu naprężenia i pola powierzchni np. ${\displaystyle -\sigma _{xx}dydz\ \mathrm {[Pa\cdot m\cdot m={\frac {N}{m^{2}}}\cdot m\cdot m=N]} }$), dla każdej ścianki, została umieszczona na rysunku z elementem sześciennym.

Wyjaśnienie wartości sił (przybliżeń i znaków minus) na ściankach sześcianu

Wyjaśnienia wymaga dlaczego przy naprężeniach na ściankach leżących na osiach współrzędnych mamy znak minus (np. na lewej ściance mamy wartość ${\displaystyle -\sigma _{xx}}$). Dla uproszczenia skupmy się na lewej ściance z naprężeniem ${\displaystyle -\sigma _{xx}.}$ Znak minus spowodowany jest tym, że wektor normalny do tej ścianki ${\displaystyle {\vec {n}}=[-1,0,0]=-{\vec {e}}_{x}}$ jest ujemnym wektorem jednostkowym. Wówczas przy obliczaniu wektora naprężenia z definicji ${\displaystyle {\vec {s}}={\vec {n}}\cdot {\boldsymbol {\sigma }}=[-\sigma _{xx},-\sigma _{xy},-\sigma _{xy}]}$ zatem składowa x tego wektora to ${\displaystyle s_{x}=-\sigma _{xx}}$ (podobne rozumowanie używamy dla naprężeń na ściance dolnej i tylnej tj.: ${\displaystyle -\sigma _{yx},-\sigma _{zx}}$). Drugim elementem wymagającym wyjaśnienia jest przybliżenie wartości naprężeń na ściankach przeciwległych do ścianek leżących na osiach. Skupmy się na ściance prawej na której naprężenie jest przybliżeniem naprężenia ${\displaystyle \sigma _{xx}}$ ze ścianki lewej w punktach o wsp. ${\displaystyle x+dx}$ i wynosi ono ${\displaystyle \sigma _{xx}+{\frac {\partial \sigma _{xx}}{\partial x}}dx.}$ To przybliżenie wzięło się z zastosowania wzoru Taylora na przybliżenie funkcji tj.: ${\displaystyle \sigma _{xx}(x+dx)=\sigma _{xx}(x)+dx{\frac {\partial \sigma _{xx}(x)}{\partial x}}+{\frac {dx^{2}}{2}}{\frac {\partial ^{2}\sigma _{xx}(x)}{\partial x^{2}}}+...}$ Ponieważ wartość ${\displaystyle dx^{2}}$ jest nieskończenie mniejsza od wartości ${\displaystyle dx}$ więc wszystkie wyrazy z ${\displaystyle dx}$ w potęgach wyższych niż jeden możemy porzucić, uznając za nieistotne (argument Leibnitza - związany z iloczynem pochodnych). W ten sposób otrzymaliśmy szukane przybliżenie naprężenia na przeciwległej ściance. Bardziej intuicyjne przedstawienie przybliżenia wartości ${\displaystyle \sigma _{xx}}$ w punkcie ${\displaystyle x+dx}$ obrazuje rysunek pod sześcianem. Podobne rozumowanie przeprowadzamy dla przybliżeń naprężeń ${\displaystyle \sigma _{yx},\sigma _{zx}}$

Sumując siły (ich składowe X) działające na każdą ze ścian, otrzymujemy:

${\displaystyle F_{p}^{x}=(\sigma _{xx}+{\frac {\partial \sigma _{xx}}{\partial x}}dx)dydz-\sigma _{xx}dydz+(\sigma _{yx}+{\frac {\partial \sigma _{yx}}{\partial y}}dy)dxdz-\sigma _{yx}dxdz+(\sigma _{zx}+{\frac {\partial \sigma _{zx}}{\partial z}}dz)dxdy-\sigma _{zx}dxdy}$

Po uporządkowaniu ${\displaystyle F_{p}^{x}}$ oraz po wykonaniu podobnego rozumowania dla składowych ${\displaystyle F_{p}^{y},F_{p}^{z}}$ (nie ma ich na rysunku – będą to wektory równoległe odpowiednio do osi Y i Z) otrzymamy:

${\displaystyle F_{p}^{x}={\frac {\partial \sigma _{xx}}{\partial x}}dxdydz+{\frac {\partial \sigma _{yx}}{\partial y}}dydxdz+{\frac {\partial \sigma _{zx}}{\partial z}}dzdxdy}$

${\displaystyle F_{p}^{y}={\frac {\partial \sigma _{xy}}{\partial x}}dxdydz+{\frac {\partial \sigma _{yy}}{\partial y}}dydxdz+{\frac {\partial \sigma _{zy}}{\partial z}}dzdxdy}$

${\displaystyle F_{p}^{z}={\frac {\partial \sigma _{xz}}{\partial x}}dxdydz+{\frac {\partial \sigma _{yz}}{\partial y}}dydxdz+{\frac {\partial \sigma _{zz}}{\partial z}}dzdxdy}$

W zapisie operatorowym możemy to wówczas zapisać:

${\displaystyle {\vec {F}}_{p}=(\nabla \cdot {\boldsymbol {\sigma }})dxdydz}$

Na wnętrze objętości kontrolnej działają siły masowe, które zapiszemy z wykorzystaniem pola przyspieszenia ${\displaystyle {\vec {f}}}$ (którym może być np. przyspieszenie ziemskie ${\displaystyle {\vec {g}}}$):

${\displaystyle {\vec {F}}_{m}=\rho {\vec {f}}dxdydz}$

Wyznaczmy pęd:

${\displaystyle {\vec {p}}=m{\vec {v}}=\rho {\vec {v}}dxdydz}$

Ponieważ założyliśmy, że badana masa jest stała więc

${\displaystyle {\frac {d{\vec {p}}}{dt}}=\rho {\frac {d{\vec {v}}}{dt}}dxdydz}$

Otrzymamy:

${\displaystyle \rho {\frac {d{\vec {v}}}{dt}}dxdydz=(\nabla \cdot {\boldsymbol {\sigma }})dxdydz+\rho {\vec {f}}dxdydz}$

Dzieląc przez ${\displaystyle dxdydz,}$ dostaniemy:

${\displaystyle \rho {\frac {d{\vec {v}}}{dt}}=\nabla \cdot {\boldsymbol {\sigma }}+\rho {\vec {f}}}$

co kończy wywód.