Teorem petala

Dalam mekanik klasik, teorem petala memberikan ringkasan dalam graviti yang boleh digunapakai pada objek-objek di dalam atau di luar satu jasad bersimetri sfera.

Isaac Newton telah memberi pembuktian teorem petala dan menyatakan bahawa:

1. Jasad tersimetri sfera memberi kesan tarikan graviti kepada objek-objek luaran seolah-olah semua jisimnya tertumpu pada satu titik di pusatnya.
2. Jika sesuatu jasad berbentuk petala bersimetri sfera (seperti bentuk bola berongga), tiada daya graviti bersih akan dikenakan pada objek di dalamnya oleh petala tersebut, tanpa mengira kedudukan objek di dalam petala tersebut.

Ekoran daripada ini, di dalam sfera pejal berketumpatan malar, daya graviti berubah secara linear mengikut jarak daripada pusat dan menjadi sifar melalui simetri di pusat jisim.

Pernyataan di atas boleh diterbitkan dengan mudah: jika satu titik dipilih di dalam sfera seperti di atas, pada jarak ${\displaystyle r}$ daripada pusat sfera, maka petala-petala berjejari lebih besar boleh tidak diambil kira mengikut teorem petala. Maka, jisim yang tinggal ${\displaystyle m}$ adalah berkadaran dengan ${\displaystyle r^{3}}$, dan daya graviti yang dikenakan padanya adalah berkadaran dengan ${\displaystyle m/r^{2}}$, yakni ${\displaystyle r^{3}/r^{2}=r}$, maka ia linear dengan ${\displaystyle r}$.

Hasil ini penting dalam analisis pergerakan planet oleh Newton; ia tidak ketara secara terus, tetapi ia boleh dibuktikan dengan kalkulus. (Sebagai alternatif, Hukum Gauss untuk graviti memberikan cara yang lebih ringkas untuk membuktikan hasil yang sama.)

Selain graviti, teorem petala boleh juga digunakan untuk menerangkan medan elektrik yang dijana oleh ketumpatan cas statik bersimetri sfera, atau sebarang fenomena lain yang mengikuti hukum kuasa dua songsang. Terbitan di bawah memfokuskan berkenaan graviti, tetapi hasil yang sama boleh diitlak dengan mudah bagi daya elektrostatik.

Sebuah jasad tersimetri sfera pejal boleh dimodel sebagai sekumpulan tidak terhingga petala-petala sfera sepusat yang tidak terhingga nipisnya. Andai salah satu petala-petala ini boleh dianggap sebagai jisim titik, maka satu sistem petala-petala (seperti jasad sfera tersebut) juga boleh dianggap sebagai jisim titik. Bayangkan satu petala sebegini:

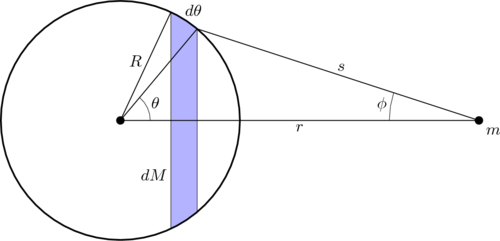
Nota: dθ dalam gambar rajah di atas merujuk kepada sudut kecil, dan bukannya panjang lengkuk. Panjang lengkuk ialah R dθ.

Menggunakan hukum kegravitian semesta Newton, jumlah daya-daya kesan daripada unsur-unsur jisim dalam jalur yang berlorek ialah:

${\displaystyle dF={\frac {Gm\;dM}{s^{2}}}.}$

Namun, oleh kerana terdapat pembatalan separa akibat sifat vektor daya ini, komponen vektor lebihan (yang menghala ke arah m) diberikan sebagai

${\displaystyle dF_{r}={\frac {Gm\;dM}{s^{2}}}\cos \phi .}$

Maka, jumlah daya pada m ialah hasil tambah daya-daya yang dikenakan oleh semua jalur. Dengan mengecilkan lebar setiap jalur, lantas menambah bilangannya, hasil tambah ini membentuk satu ungkapan kamiran:

${\displaystyle F_{r}=\int dF_{r}}$

Oleh sebab G dan m adalah malar, ia boleh dikeluarkan daripada kamiran:

${\displaystyle F_{r}=Gm\int {\frac {dM\cos \phi }{s^{2}}}.}$

Untuk menilai kamiran ini, terlebih dahulu perlu dinyatakan dM sebagai fungsi dθ.

Luas permukaan sebuah petala sfera ialah

${\displaystyle 4\pi R^{2}\,}$

manakala luas permukaan potongan nipis antara θ dan θ + dθ ialah

${\displaystyle 2\pi R^{2}\sin \theta \,d\theta }$

Jika jisim petala ialah M akan didapati bahawa

${\displaystyle dM={\frac {2\pi R^{2}\sin \theta }{4\pi R^{2}}}M\,d\theta =\textstyle {\frac {1}{2}}M\sin \theta \,d\theta }$

dan

${\displaystyle F_{r}={\frac {GMm}{2}}\int {\frac {\sin \theta \cos \phi }{s^{2}}}\,d\theta }$

Menerusi hukum kosinus,

${\displaystyle \cos \phi ={\frac {r^{2}+s^{2}-R^{2}}{2rs}}}$

${\displaystyle \cos \theta ={\frac {r^{2}+R^{2}-s^{2}}{2rR}}.}$

Kedua-dua hubungan ini menghubungkan ketiga-tiga parameter θ, s dan φ yang terdapat dalam kamiran. Apabila θ meningkat daripada 0 hingga π radian, φ berubah nilainya daripada nilai asal 0 kepada satu nilai maksimum dan akhirnya kembali ke 0 bagi θ = π.

Sebaliknya, s meningkat daripada nilai asalnya r − R ke nilai akhir r + R apabila θ meningkat daripada 0 ke π radian.

Hal ini digambarkan dalam animasi berikut:

Untuk memperoleh fungsi primitif bagi pengamir perlulah dijadikan s sebagai pembolehubah pengamiran bebas dan bukan θ.

Dengan melakukan pembezaan tersirat pada ungkapan kedua "hukum kosinus" di atas memberikan

${\displaystyle \sin \theta \;d\theta ={\frac {s}{rR}}ds.}$

dan boleh didapati bahawa

${\displaystyle F_{r}={\frac {GMm}{2rR}}\int {\frac {\cos \phi }{s}}\,ds}$

di mana pembolehubah pengamiran baru s meningkat daripada r − R ke r + R.

Dengan memasukkan ungkapan tersebut bagi cos(φ) menggunakan ungkapan "hukum kosinus" pertama, akhirnya akan diperolehi

${\displaystyle F_{r}={\frac {GMm}{4r^{2}R}}\int \left(1+{\frac {r^{2}-R^{2}}{s^{2}}}\right)\,ds.}$

Fungsi primitif pengamir ini ialah

${\displaystyle s-{\frac {r^{2}-R^{2}}{s}}}$

dan dengan meletakkan batas r − R, r + R bagi pembolehubah pengamiran s dalam fungsi primitif ini, ungkapan berikut dapat diperoleh:

${\displaystyle F_{r}={\frac {GMm}{r^{2}}},}$

yang menyatakan bahawa daya kegravitian jasad petala tersebut adalah sama dengan kegravitian satu jisim titik di pusat petala tersebut dengan jisim yang sama.

Akhir sekali, kamirkan semua petala sfera teramat nipis dengan jisim dM ini, dan kita akan memperoleh jumlah kesan graviti satu sfera pejal kepada satu objek di luar sfera tersebut

${\displaystyle F_{total}=\int dF_{r}={\frac {Gm}{r^{2}}}\int dM.}$

Antara jejari x hingga x + dx, dM boleh dinyatakan sebagai fungsi x, misalnya,

${\displaystyle dM={\frac {4\pi x^{2}dx}{{\frac {4}{3}}\pi R^{3}}}M={\frac {3Mx^{2}dx}{R^{3}}}}$

Oleh itu, jumlah keseluruhan graviti ialah

${\displaystyle F_{total}={\frac {3GMm}{r^{2}R^{3}}}\int _{0}^{R}x^{2}dx={\frac {GMm}{r^{2}}}}$

yang menyatakan bahawa daya graviti satu sfera pejal terhadap satu objek luar boleh diringkaskan sebagai daya daripada satu jisim titik di pusat bola tersebut dengan jisim yang serupa.