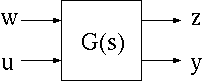H∞制御理論

${\displaystyle H^{\infty }}$制御理論（エイチインフィニティせいぎょりろん、英語：H-infinity control theory）は、外乱信号の影響を抑制する制御系を構築するための制御理論である。この制御理論は、1980年代に研究が進み、1989年頃に完成した。${\displaystyle H^{\infty }}$ノルムと呼ばれるノルムによって伝達関数を評価し、それが所望の値より小さくなるようにすることにより、目的の性能を達成させる。具体的には、一般化プラントと呼ばれる制御入力、外乱入力、制御出力、評価出力の 4 つの入出力を持つ汎用的な制御モデルを対象に、制御出力から制御入力に適切なフィードバックを施すことで外乱入力から評価出力までの伝達関数の H^∞ノルムを小さくするという制御系設計手順を取る。制御対象の不確定な部分を外乱信号として扱うことで、モデルの不確かさの影響を抑制する制御系となる。このように、想定していたモデル（ノミナルモデルと呼ぶ）からの誤差に対しても有効な（安定性を失わない） 性質をロバスト性（堅牢性、安定性）と呼ぶ。

それまでの現代制御論はモデルが正確であることを前提としていたため、モデル化誤差のあるシステムに対して性能を保証しなかったが、H^∞制御はロバスト性により多少いいかげんな同定でも許されるようになったこと、周波数領域での設計ができるようになったために古典制御に慣れた技術者が容易に設計できることなどから、産業界で積極的に採り入れられ、理論と現場の距離を縮めたと言われている。

${\displaystyle H^{\infty }}$ノルム (H-infinity norm)

伝達関数の評価指標であり、入力が出力におよぼす最大の（入力が外乱であれば最悪の）影響を見積もることができる。${\displaystyle H^{\infty }}$は、伝達関数の Hardy 空間${\displaystyle H^{\infty }}$におけるノルムを評価規範としていることに由来する。伝達関数${\displaystyle G\in H^{\infty }}$の${\displaystyle H^{\infty }}$ノルムは、全周波数領域における最大特異値と定義される。

${\displaystyle \|G\|_{\infty }=\sup _{\omega }\sigma (G(j\omega )).}$

ただし${\displaystyle \sigma (\cdot )}$ は最大特異値である。特に伝達関数がスカラーである場合は全周波数領域におけるゲインの上界となる。

${\displaystyle \|G\|_{\infty }=\sup _{\omega }|G(j\omega )|.}$

一般化プラント (generalized plant)

制御入力 ${\displaystyle u}$, 外乱入力 ${\displaystyle w}$, 制御出力 ${\displaystyle y}$, 評価出力 ${\displaystyle z}$ の 4 つの入出力を持つ、汎用的な制御モデルである。

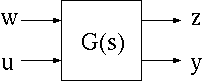
この系は、下図のようなフィードバック則 ${\displaystyle u=Ky}$ を適用することを前提としている。

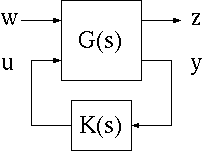
補償器 ${\displaystyle K}$ を適当に選ぶことで外乱入力 ${\displaystyle w}$ から評価出力 ${\displaystyle z}$ までの伝達関数の H^∞ノルム ${\displaystyle \|G_{zw}\|_{\infty }}$ を望みの値より小さくすることができれば、最悪外乱に対して所望の外乱抑制効果を保証することができる。

状態空間表現では

${\displaystyle {\begin{matrix}{\dot {x}}&=&Ax+B_{1}w+B_{2}u\\z&=&C_{1}x+D_{11}w+D_{12}u\\y&=&C_{2}x+D_{21}w+D_{22}u\end{matrix}}}$

のように表される。

小ゲイン定理 (small gain theorem)

閉ループ系の構成要素となる各ブロックの積の H^∞ノルムが 1 未満であれば、閉ループ系は安定であるという定理。

混合感度問題 (mixed sensitivity problem)

正規化既約分解 (normalized coprime factorization)

標準問題 (standard problem)

プロパーな制御器 ${\displaystyle u=K(s)y}$ によって、与えられた ${\displaystyle \gamma }$ について、ノルム条件

${\displaystyle \|G\|_{\infty }<\gamma }$

を満たす ${\displaystyle K(s)}$ を見出す問題。${\displaystyle \gamma }$ が小さければ小さいほど外乱抑制性能が優れていることになる。2 次のリッカチ方程式を解く問題に帰着されるが、一般に解析的な解が得られないため、与えられた ${\displaystyle \gamma }$ について可解であるかどうかは、リッカチ方程式を解いてみるまで分からない。

ガンマイタレーション (Gamma Iteration)

繰り返し標準問題を解くことによって、ノルム条件を満たす最小の ${\displaystyle \gamma }$ を極値探索法で見つけること。これにより制御器を得ることを H^∞最適制御問題と呼ぶ。

• 制御理論
  • 線形システム論
  • 最適制御理論