Rete di Zobel

La rete di Zobel è un tipo di filtro basato sul principio della immagine d'impedenza. Il nome deriva dal suo inventore Otto Julius Zobel del Bell Labs, che pubblicò opere sul tema nel 1923.^[1] La caratteristica della rete di Zobel è di avere una impedenza d'ingresso costante indipendentemente dalla funzione di trasferimento. Questo è possibile al costo di implementare più sezioni di filtro e quindi componenti rispetto ad altri filtri. L'impedenza è nominalmente costante e resistiva pura. Per questo motivo le reti di Zobel sono anche dette a resistenza costante. Qualunque impedenza può essere implementata con componenti discreti.

Le reti di Zobel sono largamente utilizzate nelle telecomunicazioni per appiattire e allargare le risposte in frequenza di linee di rame terrestri, aumentando la qualità delle linee telefoniche. L'uso è calato con il passaggio ai sistemi digitali che hanno soppiantato quelli analogici.

Quando utilizzato per cancellare la parte reattiva dell'impedenza di un altoparlante viene chiamato a volte cella di Boucherot. In questo caso, solo metà della rete è implementata con componenti discreti, mentre l’altra parte è formata dal circuito equivalente del trasduttore. È usata anche per la correzione del fattore di potenza nella distribuzione di corrente elettrica, ecco l'associazione al nome Boucherot.

Una configurazione tipica di una rete di Zobel è quella con ponte a T.

La base della rete di Zobel è un ponte bilanciato come mostrato in figura. La condizione di bilanciamento è;

${\displaystyle {\frac {Z}{Z_{0}}}={\frac {Z_{0}}{Z'}}}$

Se questo è espresso in termini di una normalizzata Z₀ = 1 come convenzionalmente fatto nelle tavole di filtri, la condizione di bilanciamento è semplice;

${\displaystyle Z={\frac {1}{Z'}}}$

In altre parole, ${\displaystyle \scriptstyle Z'}$ è semplicemente l'inverso, o impedenza duale di ${\displaystyle \scriptstyle Z}$.

L'impedenza del ponte Z_B è attraverso i punti bilanciati e nessun potenziale lo attraversa. Conseguentemente, non vi è corrente che attraversa e il suo valore non fa differenza alla funzione del circuito. Comunque solitamente il suo valore scelto è Z₀ per ragioni che si evincono nella configurazione a T.

L'impedenza d'ingresso è data da

${\displaystyle {\frac {1}{Z_{\text{in}}}}={\frac {1}{Z_{0}+Z'}}+{\frac {1}{Z+Z_{0}}}}$

Sostituendo la condizione di bilanciamento,

${\displaystyle Z'={\frac {Z_{0}^{2}}{Z}}}$

si ottiene

${\displaystyle Z_{\text{in}}=Z_{0}}$

La impedenza d'ingresso può essere progettata resistiva pura settando

${\displaystyle Z_{0}=R_{0}\!\,}$

L'impedenza d'ingresso sarà quindi reale e indipendente da ω in banda e fuori banda indipendentemente dalla complessità delle sezioni del filtro scelte.

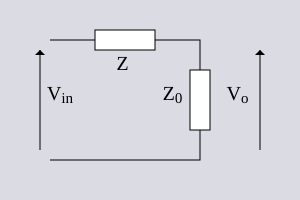
Se Z₀ nella parte sotto a destra del circuito è preso come carico sull'uscita allora la funzione di trasferimento di V_in/V_o può essere calcolata per la sezione. Solo il ramo rhs deve essere considerato per il calcolo. La ragione di questo è da trovare nel fatto che non vi è corrente che scorre attraverso R_B. Nessuna corrente scorre attraverso il ramo lhs verso il carico. Il ramo lhs non può avere effetto sull'uscita. È certamente influenzata l'impedenza d'ingresso (e il voltaggio all'ingresso) ma non la funzione di trasferimento. La funzione di trasferimento è quindi;

${\displaystyle A(\omega )={\frac {Z_{0}}{Z+Z_{0}}}}$

L'impedenza del carico è l'impedenza delle sezioni o della linea di trasmissione e può essere omessa dal circuito. Se settiamo;

${\displaystyle Z_{B}=Z_{0}\,\!}$

il circuito sulla destra risulta. Questo si riferisce a un ponte a T perché l'impedenza Z è vista dal "ponte" attraverso la sezione a T. Lo scopo di susare Z_B = Z₀ è di rendere simmetrica la sezione del filtro. Questo ha il vantaggio di avere la stessa impedenza, Z₀, sia in ingresso che in uscita.

Unn filtro Zobel può essere implementato come passa basso, passa alto, passa banda o elimina banda. È possibile anche implementare un filtro a risposta piatta di attenuazione.

Per una sezione che faccia da attenuatore, Z è semplicemente

${\displaystyle Z=R\,\!}$

e

${\displaystyle Z'=R'={\frac {R_{0}^{2}}{R}}}$

L'attenuazione è data da;

${\displaystyle L=20\log \left({\frac {R}{R_{0}}}+1\right)\,{\text{dB}}}$

Per una sezione passa basso, Z è un induttore e Z ' è una capacità;

${\displaystyle Z=i\omega L\!\,}$

e

${\displaystyle Z'={\frac {1}{i\omega C'}}}$

dove

${\displaystyle C'={\frac {L}{R_{0}^{2}}}}$

La funzione di trasferimento è data

${\displaystyle A(\omega )={\frac {R_{0}}{i\omega L+R_{0}}}}$

Il punto 3 dB si ha quando ωL = R₀ così i 3 dB di cut-off è dato da

${\displaystyle \omega _{c}={\frac {R_{0}}{L}}}$

dove ω è nella banda eliminata circa ω_c,

${\displaystyle A(\omega )\approx {\frac {R_{0}}{i\omega L}}}$

può essere visto da A(ω) calando lontano nell abanda eliminata a 6 dB/ottava (o 20 dB/decade).

Per un filtro passa alto, Z è una capacità e Z' un induttore:

${\displaystyle Z={\frac {1}{i\omega C}}}$

e

${\displaystyle Z'=i\omega L'\!\,}$

dove

${\displaystyle L'=CR_{0}^{2}\!\,}$

La funzione di trasferimento della sezione è data da

${\displaystyle A(\omega )={\frac {i\omega CR_{0}}{1+i\omega CR_{0}}}}$

Il punto 3 dB occorre quando ωC = ¹⁄_R0 così la frequenza a 3 dB cut-off è data da

${\displaystyle \omega _{c}={\frac {1}{CR_{0}}}}$

In elimina banda,

${\displaystyle A(\omega )\approx i\omega CR_{0}}$

Per una sezione passa banda, Z è una serie di circuiti risonanti e Z' è un o shunt risonante;

${\displaystyle Z=i\omega L+{\frac {1}{i\omega C}}}$

e

${\displaystyle Y'={\frac {1}{Z'}}=i\omega C'+{\frac {1}{i\omega L'}}}$

La funzione di trasferimento è data da

${\displaystyle A(\omega )={\frac {i\omega CR_{0}}{1+i\omega CR_{0}-\omega ^{2}LC}}}$

Il punto 3 dB occorre quando |1 − ω²LC| = ωCR₀ così la frequenza a 3 dB cut-off è data da

${\displaystyle \omega _{c}={\frac {1}{2LC}}\left(\pm R_{0}C+{\sqrt {R_{0}^{2}C^{2}+4LC}}\right)}$

dal centro frequenza, ω_m, e larghezza di banda, Δω, può essere determinata:

${\displaystyle {\begin{aligned}\Delta \omega &={\frac {R_{0}}{L}}\\\omega _{m}&={\sqrt {{\frac {R_{0}^{2}}{4L^{2}}}+{\frac {1}{LC}}}}\end{aligned}}}$

Nota questo è differente dalla frequenza di risonanza

${\displaystyle \omega _{0}={\sqrt {\frac {1}{LC}}}}$

la relazione tra loro inizia da

${\displaystyle \omega _{m}^{2}=\left({\frac {\Delta \omega }{2}}\right)^{2}+\omega _{0}^{2}}$

Per una sezione elimina banda, Z è uno shunt risonante e Z' è una serie risonante

${\displaystyle Y={\frac {1}{Z}}=i\omega C+{\frac {1}{i\omega L}}}$

e

${\displaystyle Z'=i\omega L'+{\frac {1}{i\omega C'}}}$

La funzione di trasferimento e la larghezza di banda può essere trovata in analogia con la sezione passa banda.

${\displaystyle \Delta \omega ={\frac {1}{CR_{0}}}}$

e,

${\displaystyle \omega _{m}={\sqrt {\left({\frac {1}{2R_{0}C}}\right)^{2}+{\frac {1}{LC}}}}}$

• Otto Julius Zobel
• Filtro (elettronica)
• Impedenza immagine
• Filtro a costante k
• Cella di Boucherot
• Equalizzatore dei ritardi con ponte a T

• Wikimedia Commons contiene immagini o altri file su Rete zobel