Graphe biparti complet

Cet article ne cite pas suffisamment ses sources (mai 2014).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

Graphe biparti complet
${\displaystyle K_{3,2}}$
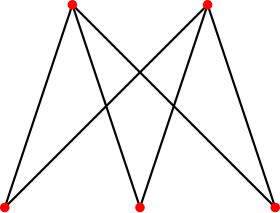Notation	${\displaystyle K_{m,n}}$
Nombre de sommets	${\displaystyle m+n}$
Nombre d'arêtes	${\displaystyle mn}$
Distribution des degrés	m sommets de degré n n sommet de degré m
Diamètre	2
modifier

En théorie des graphes, un graphe est dit biparti complet (ou encore est appelé une biclique) s'il est biparti et chaque sommet du premier ensemble est relié à tous les sommets du second ensemble. Plus précisément, il existe une partition de son ensemble de sommets en deux sous-ensembles ${\displaystyle U}$ et ${\displaystyle V}$ telle que chaque sommet de ${\displaystyle U}$ est relié à chaque sommet de ${\displaystyle V}$^{[réf. nécessaire]}.

Si le premier ensemble ${\displaystyle U}$ est de cardinal m et le second ensemble ${\displaystyle V}$ est de cardinal n, le graphe biparti complet est noté ${\displaystyle K_{m,n}}$.

Si m = 1, le graphe complet biparti K_1,n est une étoile et est noté ${\displaystyle S_{n}}$^{[réf. nécessaire]}.

En particulier, les étoiles sont des arbres. D'ailleurs, tous les graphes bipartis complets qui sont des arbres sont des étoiles^{[réf. nécessaire]}.

Voici des exemples pour m = 3.

• 
  K_3,1
• 
  K_3,2
• 
  K_3,3

Le graphe K_3,3 est le plus petit graphe cubique non planaire^{[réf. nécessaire]}. Il sert dans les caractérisation des graphes planaires de Kazimierz Kuratowski et de Klaus Wagner^{[réf. nécessaire]}. C'est lui qui réside derrière l'énigme des trois maisons.

• Le graphe biparti complet ${\displaystyle K_{n,n}}$ est un graphe de Moore et une ${\displaystyle (n,4)}$-cage^{[réf. nécessaire]}.
• Les graphes bipartis complets ${\displaystyle K_{n,n}}$ et ${\displaystyle K_{n,n+1}}$ sont des graphes de Turán^{[réf. nécessaire]}.
• Le graphe biparti complet ${\displaystyle K_{n,n}}$ est un graphe symétrique : il est arête-transitif, sommet-transitif et arc-transitif^{[réf. nécessaire]}.
• Le nombre d'arbres couvrants du graphe biparti complet ${\displaystyle K_{m,n}}$ est ${\displaystyle m^{n-1}n^{m-1}}$ ^[1].

Le polynôme caractéristique du graphe biparti complet ${\displaystyle K_{m,n}}$ est : ${\displaystyle x^{m+n-2}(x^{2}-mn)}$^{[réf. nécessaire]}. Ce polynôme caractéristique n'admet que des racines entières si, et seulement si, mn est un carré parfait. Le graphe biparti complet n'est donc un graphe intégral que dans ce cas.

Le théorème de Kuratowski qui caractérise les graphes planaires utilise le graphe ${\displaystyle K_{3,3}}$^[2],[3].

On note ${\displaystyle \mathrm {cr} (G)}$ le nombre de croisements du graphe ${\displaystyle G}$, le nombre minimal de croisements parmi les tracés possibles de ${\displaystyle G}$. Kazimierz Zarankiewicz^[4], voulant résoudre le problème de l'usine de briques de Pál Turán, a établi la majoration suivante :

${\displaystyle {\textrm {cr}}(K_{m,n})\leq \left\lfloor {\frac {n}{2}}\right\rfloor \left\lfloor {\frac {n-1}{2}}\right\rfloor \left\lfloor {\frac {m}{2}}\right\rfloor \left\lfloor {\frac {m-1}{2}}\right\rfloor }$

Cette inégalité est conjecturée être une égalité^[5].

Étant donné un graphe G, trouver le sous-graphe induit biparti complet ${\displaystyle K_{m,n}}$ de G avec le plus possible d'arêtes (donc avec ${\displaystyle mn}$ maximal) est un problème NP-complet^{[réf. nécessaire]}.

Théorème de Graham-Pollak

• Portail des mathématiques