Fonction affine

En analyse, une fonction affine est une fonction obtenue par addition et multiplication de la variable par des constantes. Elle peut donc s'écrire sous la forme :

${\displaystyle f(x)=ax+b}$

où les paramètres ${\displaystyle a}$ et ${\displaystyle b}$ ne dépendent pas de ${\displaystyle x}$^[1].

Lorsque la fonction est définie sur l'ensemble des réels, elle est représentée par une droite, dont ${\displaystyle a}$ est la pente et ${\displaystyle b}$ l'ordonnée à l'origine.

Un cas particulier des fonctions affines est lorsque l'ordonnée à l'origine est nulle, on obtient alors une fonction linéaire.

Les fonctions constantes et linéaires sont des exemples de fonctions affines. Les fonctions affines sont elles-mêmes des exemples de fonctions polynomiales de degré inférieur ou égal à 1.

La notion de fonction affine est généralisée en géométrie par celle d'application affine.

Remarque : dans certaines branches des mathématiques comme la statistique^[2], une telle fonction est appelée, à l'image du terme anglophone linear function et du terme allemand Lineare Funktion, une fonction linéaire en référence au fait que son graphe est une ligne droite.

Propriété caractéristique

Une fonction affine ${\displaystyle f}$ est caractérisée par le fait que son taux d'accroissement est constant. C'est-à-dire qu'il y a proportionnalité entre les accroissement de ${\displaystyle x}$ et les accroissement de ${\displaystyle f(x)}$. En effet, si ${\displaystyle x_{1}}$ et ${\displaystyle x_{2}}$ sont deux réels, l'accroissement ${\displaystyle f(x_{1})-f(x_{2})=a(x_{1}-x_{2})}$ est proportionnel à ${\displaystyle x_{1}-x_{2}}$. Le coefficient de proportionnalité est ${\displaystyle a}$.

Une fonction ${\displaystyle f}$ est affine si et seulement si il existe ${\displaystyle a}$ tel que pour tout réels ${\displaystyle x_{1},x_{2}}$, ${\displaystyle f(x_{1})-f(x_{2})=a(x_{1}-x_{2})}$.

Cette propriété donne alors un outil pour déterminer le coefficient ${\displaystyle a}$ :

${\displaystyle a={\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}}$ si ${\displaystyle x_{1}\neq x_{2}}$.

On en déduit : ${\displaystyle f'(x)=a}$. La dérivée d'une fonction affine est une fonction constante dont la valeur est le coefficient multiplicateur — ou coefficient de proportionnalité — de la fonction affine.

L'ordonnée à l'origine ${\displaystyle b}$ peut se calculer de la manière suivante :

${\displaystyle b={\frac {x_{2}f(x_{1})-x_{1}f(x_{2})}{x_{2}-x_{1}}}}$ si ${\displaystyle x_{1}\neq x_{2}}$.

Si l'on connaît l'expression de ${\displaystyle f}$, alors on a que ${\displaystyle b=f(0)}$.

Résolution d'équations et d'inéquations

Supposons ${\displaystyle a,b}$ réels et ${\displaystyle a}$ non nul.

• L'unique solution de l'équation ${\displaystyle ax+b=0}$ est le réel ${\displaystyle -{\frac {b}{a}}}$.
• L'ensemble des solutions de l'inéquation ${\displaystyle ax+b\geq 0}$ est l'intervalle réel ${\displaystyle \left[-{\frac {b}{a}},+\infty \right[}$ si ${\displaystyle a>0}$, ${\displaystyle \left]-\infty ,-{\frac {b}{a}}\right]}$ si ${\displaystyle a<0}$.

Exemples

• Exemple de l'abonnement téléphonique.

Le prix de l'abonnement mensuel est ${\displaystyle A}$ et le prix d'une communication à la minute est de 0,10 €/min. La facture téléphonique est alors une fonction affine du nombre ${\displaystyle x}$ de minutes de communication dans le mois :

${\displaystyle f\,\colon x\mapsto A+0{,}1~x}$.

• Longueur d'un ressort.

Si au repos le ressort a une longueur ${\displaystyle L_{0}}$ et si sa raideur est ${\displaystyle k}$, alors la longueur du ressort est une fonction affine de la force appliquée (loi de Hooke).

${\displaystyle L\,\colon f\mapsto L_{0}+{\frac {f}{k}}}$.

Dans ce cas, le coefficient directeur est ${\displaystyle 1/k}$ et l'ordonnée à l'origine ${\displaystyle L_{0}}$.

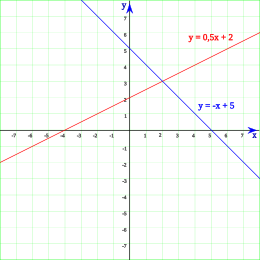
Représentation graphique

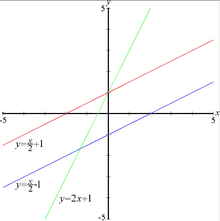
La représentation graphique d'une fonction affine définie sur l'ensemble des réels est une droite^[4] dont l'équation est

${\displaystyle y=ax+b}$.

La droite coupe l'axe des ordonnées pour ${\displaystyle y=b}$ (d'où le nom d'ordonnée à l'origine)^[4]. Lorsque ${\displaystyle b}$ est nul, la droite passe par l'origine du repère cartésien.

La droite a pour « pente » ou « coefficient directeur » le réel ${\displaystyle a}$^[4]. Si ${\displaystyle a>0}$, la fonction affine est croissante (la droite « monte ») et si ${\displaystyle a<0}$, elle est décroissante (la droite « descend »). Par un processus analogue à celui vu pour la fonction linéaire, un déplacement d'un carreau en abscisse induit un déplacement de ${\displaystyle a}$ carreaux en ordonnée, si le repère est orthonormé.

Détermination des coefficients

Si ${\displaystyle M(x_{1},y_{1})}$ et ${\displaystyle N(x_{2},y_{2})}$ sont deux points distincts appartenant à la droite d'équation ${\displaystyle y=ax+b}$, alors :

${\displaystyle a={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}}$,

${\displaystyle b=y_{1}-ax_{1}=y_{2}-ax_{2}={\frac {x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}}$.

Si ${\displaystyle a=0}$ alors la fonction est constante et si ${\displaystyle b=0}$ alors la fonction est linéaire.

Notes et références

Voir aussi

Articles connexes

• Application affine (d'un espace affine dans un autre)
• Fonction affine par morceaux

Bibliographie

• Jean Wacksmann, Mathématiques - Seconde : Pour aller plus loin en démontrant et en s’entraînant, Ellipses, 8 janvier 2019, 576 p. (ISBN 9782340028708), chap. 6.1 (« Fonction affine »)

• Portail de l'analyse