Degré de liberté (physique)

Pour les articles homonymes, voir Degré de liberté.

Cet article ne cite pas suffisamment ses sources (octobre 2021).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

En physique, un degré de liberté (abrégé ddl ou DDL) est un paramètre indépendant dans la description formelle de l'état d'un système physique, ou peut-être plus précisément d'un système dynamique. Le terme paramètre est à prendre ici au sens large, comme un élément d'information, généralement un nombre, identifié à une grandeur physique. De manière cruciale, ce paramètre doit avoir la liberté d'évoluer sans contraintes.

Ce concept très général de degré de liberté est utilisé dans de nombreux domaines de la physique (mécanique, physique statistique, chimie, théorie quantique des champs, ...), ainsi qu'en mathématiques pures (statistique). Nous listons quelques exemples dans cette section.

En génie mécanique, les degrés de liberté indiquent les différentes possibilités de mouvement dans l'espace. Se référer à l'article degré de liberté (génie mécanique). Cette utilisation de l'expression est similaire à celle utilisée dans la typologie des vibrations moléculaires. Dans le dernier cadre évoqué (description des mouvements moléculaires), deux types de degrés de liberté sont identifiés : les degrés de liberté externes au nombre de 6, correspondant aux mouvements de la molécule dans l'espace (translations et rotations), et les degrés de liberté internes, correspondant aux déformations de la molécule par rapport à sa conformation d'équilibre.

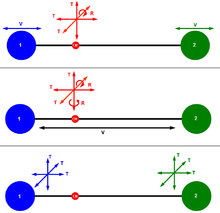
En trois dimensions, il existe 6 degrés de liberté associés au mouvement d'une particule, 3 pour sa position, 3 pour sa quantité de mouvement. Il existe donc 6 degrés de liberté au total. Une autre façon de justifier ce schéma est de considérer que le mouvement de la molécule sera décrit par le mouvement de deux particules mécaniques représentant ses deux atomes, que 6 degrés de liberté sont attachés à chaque particule, comme ci-dessus. Avec cette autre considération, il apparaît que différents ensembles de degrés de liberté peuvent être définis afin de définir le mouvement de la molécule. En fait les degrés de liberté pour un système mécanique est un ensemble d'axes indépendants dans l'espace des phases du système, ce qui permet de le générer entièrement. Pour un espace multidimensionnel comme l'espace des phases, il existe plus d'un ensemble possible d'axes. Il est établi que tous les degrés de liberté de la molécule d'hydrogène ne participent pas à l'expression de son énergie. Par exemple, les degrés associés à la position du centre de masse n'y participent pas.

Dans le tableau ci-dessous, les degrés négligés le sont en raison de leur faible influence sur l'énergie totale, à moins d'être à très hautes températures ou énergies. La rotation diatomique est négligée en raison de la rotation autour des axes moléculaires. La rotation monoatomique est négligée pour la même raison que la diatomique, mais cet effet est valable dans les deux autres directions.

Dans le modèle de chaîne idéale, deux angles sont nécessaires pour décrire l'orientation de chaque monomère.

En physique statistique, un degré de liberté est un nombre unique décrivant un micro-état d'un système. La spécification de tous les micro-états d'un système est un point dans l'espace de phase du système.

La description de l'état d'un système en tant que point dans son espace de phase, bien que mathématiquement pratique, est fondamentalement inexacte. En mécanique quantique, les degrés de liberté de mouvement sont remplacés (dans la représentation de Schrödinger) par le concept de fonction d'onde et les opérateurs qui correspondent à d'autres degrés de liberté ont des spectres discrets. Par exemple, l'opérateur de spin d'un électron ou d'un photon n'a que deux valeurs propres. Cette discontinuité devient apparente lorsque l'action a un ordre de grandeur proche de la constante de Planck et que les degrés de liberté individuels peuvent être distingués.

(Voir aussi la discussion sur les degrés de liberté dans l'article sur la mécanique quantique dans la représentation de Heisenberg.)

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

L'ensemble de degrés de liberté ${\displaystyle X_{1},\ldots ,X_{N}}$ d'un système est indépendant si l'énergie associée avec l'ensemble peut être écrite sous la forme suivante :

${\displaystyle E=\sum _{i=1}^{N}E_{i}(X_{i}),}$

où ${\displaystyle E_{i}}$ est une fonction de la seule variable ${\displaystyle X_{i}}$.

Exemple : si ${\displaystyle X_{1}}$ et ${\displaystyle X_{2}}$ sont deux degrés de liberté, et ${\displaystyle E}$ est l'énergie associée :

• si ${\displaystyle E=X_{1}^{4}+X_{2}^{4}}$, alors les deux degrés de liberté sont indépendants ;
• si ${\displaystyle E=X_{1}^{4}+X_{1}X_{2}+X_{2}^{4}}$, les deux degrés de liberté ne sont pas indépendants. Le terme impliquant le produit de ${\displaystyle X_{1}}$ et ${\displaystyle X_{2}}$ est un terme de couplage, qui décrit une interaction entre deux degrés de liberté.

Si ${\displaystyle X_{1},\ldots ,X_{N}}$ est un ensemble de degrés de liberté indépendants alors, à l'équilibre thermodynamique, ${\displaystyle X_{1},\ldots ,X_{n}}$ sont statistiquement indépendants les uns des autres.

Pour i de 1 à N, la valeur du i^e degré de liberté ${\displaystyle X_{i}}$ est distribué selon une loi de Boltzmann. Sa fonction de densité de probabilité est la suivante :

${\displaystyle p_{i}(X_{i})={\frac {e^{-{\frac {E_{i}}{k_{B}T}}}}{\int dX_{i}\,e^{-{\frac {E_{i}}{k_{B}T}}}}}}$,

Dans cette section, et par la suite, les ${\displaystyle \langle \rangle }$ indiquent la moyenne de la quantité qu'ils entourent.

L'énergie interne du système est la somme des énergies moyennes associées à chacun des degrés de liberté :

${\displaystyle U=\langle E\rangle =\sum _{i=1}^{N}\langle E_{i}\rangle }$ .

Un degré de liberté ${\displaystyle X_{i}}$ est quadratique si les termes d'énergie associés peuvent être écrits :

${\displaystyle E=\alpha _{i}\,\,X_{i}^{2}+\beta _{i}\,\,X_{i}Y}$,

où ${\displaystyle Y}$ est une combinaison linéaire d'autres degrés de liberté quadratiques.

Par exemple, si ${\displaystyle X_{1}}$ et ${\displaystyle X_{2}}$ sont deux degrés de liberté, et ${\displaystyle E}$ l'énergie associé :

• Si ${\displaystyle E=X_{1}^{4}+X_{1}^{3}X_{2}+X_{2}^{4}}$, alors les deux degrés de liberté ne sont pas indépendants et ne sont pas quadratiques.
• Si ${\displaystyle E=X_{1}^{4}+X_{2}^{4}}$, les degrés de liberté sont indépendants et non quadratiques.
• Si ${\displaystyle E=X_{1}^{2}+X_{1}X_{2}+2X_{2}^{2}}$, les degrés de liberté ne sont pas indépendants et sont quadratiques.
• Si ${\displaystyle E=X_{1}^{2}+2X_{2}^{2}}$, les degrés de liberté sont indépendants et quadratiques.

En mécanique classique, la dynamique d'un système de degrés de liberté quadratiques est contrôlée par un ensemble d'équations différentielles linéaires avec des coefficients constants.

${\displaystyle X_{1},\ldots ,X_{N}}$ sont des degrés de liberté quadratiques et indépendants si l'énergie associée à un micro-état du système qu'ils décrivent peut être écrite :

${\displaystyle E=\sum _{i=1}^{N}\alpha _{i}X_{i}^{2}}$.

En physique statistique classique, à l'équilibre thermodynamique, l'énergie interne d'un système de N degrés de liberté indépendants et quadratiques est :

${\displaystyle U=\langle E\rangle =N\,{\frac {k_{B}T}{2}}}$.

• Entropie
• Variance (thermodynamique)

• Portail de la physique
• Portail de la chimie