Grafo de Turán

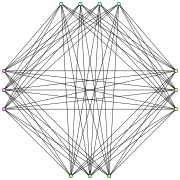El grafo de Turán ${\displaystyle T(13,4)}$
Nombre en honor a	Pál Turán
Vértices	${\displaystyle n}$
Aristas	${\displaystyle \sim {\frac {(r-1)n^{2}}{2r}}}$
Radio	${\displaystyle \left\{{\begin{array}{ll}\infty &r=1\\2&r\leq n/2\\1&{\text{de otra manera}}\end{array}}\right.}$
Diámetro	${\displaystyle \left\{{\begin{array}{ll}\infty &r=1\\1&r=n\\2&{\text{de otra manera}}\end{array}}\right.}$
Cintura	${\displaystyle \left\{{\begin{array}{ll}\infty &r=1\vee (n\leq 3\wedge r\leq 2)\\4&r=2\\3&{\text{de otra manera}}\end{array}}\right.}$
Número cromático	${\displaystyle r}$
Notación	${\displaystyle T(n,r)}$
[editar datos en Wikidata]

El grafo de Turán ${\displaystyle T(n,r)}$ es un grafo multipartito completo formado por el posicionamiento de un conjunto de ${\displaystyle n}$ vértices dentro de ${\displaystyle r}$ subconjuntos, con tamaños lo más iguales posibles, y conectando dos vértices por una esquina sí y solo sí estos pertenecen a subconjuntos diferentes. El grafo tendrá ${\displaystyle (n\,{\bmod {\,}}r)}$ conjuntos de ${\displaystyle \lceil n/r\rceil }$ tamaño, y ${\displaystyle r-(n\,{\bmod {\,}}r)}$ subconjuntos de ${\displaystyle \lfloor n/r\rfloor }$ tamaño. Es decir, un grafo ${\displaystyle r}$-partito completo

${\displaystyle K_{\lceil n/r\rceil ,\lceil n/r\rceil ,\ldots ,\lfloor n/r\rfloor ,\lfloor n/r\rfloor }.}$

Cada vértice tiene grados o de ${\displaystyle n-\lceil n/r\rceil }$ o de ${\displaystyle n-\lfloor n/r\rfloor }$. El número de esquinas es

${\displaystyle {\frac {1}{2}}(n^{2}-(n\,{\bmod {\,}}r)\lceil n/r\rceil ^{2}-(r-(n\,{\bmod {\,}}r))\lfloor n/r\rfloor ^{2})\leq \left(1-{\frac {1}{r}}\right){\frac {n^{2}}{2}}.}$

Se convierte en un grafo regular cuando ${\displaystyle n}$ es divisible por ${\displaystyle r}$.

Los grafos de Turán deben su nombre Pál Turán, quien los utilizó para probar el teorema de Turán, un importante resultado en la teoría de grafos extremales.^[1]​

Por el principio de Dirichlet, cada conjunto de ${\displaystyle r+1}$ vértices en el grafo de Turán incluyen dos vértices en el mismo subconjunto de partición; por lo tanto, el grafo de Turán no contiene un clique de tamaño ${\displaystyle r+1}$. De acuerdo al teorema de Turán, el grafo de Turán tiene el máximo número posible de esquinas entre todo grafo libre de clique ${\displaystyle (r+1)}$ con ${\displaystyle n}$ vértices. Keevash y Sudakov, en 2003, demostraron que el grafo de Turán es el único grafo libre de clique ${\displaystyle (r+1)}$ de orden ${\displaystyle n}$, en el cual cada subconjunto de ${\displaystyle \alpha n}$ vértices se extiende al menos ${\displaystyle {\frac {r\,{-}\,1}{2r}}(2\alpha -1)n^{2}}$ esquinas, si ${\displaystyle \alpha }$ está lo suficientemente cerca de 1.^[2]​ El teorema de Erdős–Stone extiende al teorema de Turán limitando el número de aristas en un grafo que no tiene un grafo de Turán arreglado como un subgrafo. A través de este teorema, límites similares en la teoría de grafos extremales puede ser probada para cada subgrafo excluido, dependiendo en el número cromático del subgrafo.

Varias opciones del parámetro ${\displaystyle r}$ en un grafo de Turán dirigen a notables grafos que han sido estudiados independientemente.

El grafo de Turán ${\displaystyle T(2n,n)}$ puede ser formado removiendo el emparejamiento perfecto de un grafo completo ${\displaystyle K_{2n}}$. Como mostró Roberts en 1969, este grafo tiene una boxicidad de exactamente ${\displaystyle n}$; es a veces conocido como el grafo de Roberts.^[3]​ Este grafo es también el 1-esqueleto de un ortoplex ${\displaystyle n}$-dimensional; por ejemplo, el grafo ${\displaystyle T(6,3)=K_{2,2,2}}$ es el grafo octahédrico, el grafo de un octaedro regular. Si ${\displaystyle n}$ parejas van a una fiesta, y cada persona se aprieta de manos con cada persona a excepción de su pareja, entonces este grafo describe el conjunto de apretones de manos que tomaron lugar; por esta razón es también llamado el grafo de veladas (del inglés cocktail party graph).

El grafo de Turán ${\displaystyle T(n,2)}$ es un grafo bipartito completo y, cuando ${\displaystyle n}$ es par, un grafo de Moore. Cuando ${\displaystyle r}$ es divisor de ${\displaystyle n}$, el grafo de Turán es simétrico y fuertemente regular, a pesar de que algunos autores consideran a los grafos de Turán ser un caso trivial de fuerte regularidad y por lo tanto los excluyen de la definición de un grafo fuertemente regular.

El grafo de Turán ${\displaystyle T(n,\lceil n/3\rceil )}$ tiene ${\displaystyle 3^{a}2^{b}}$ cliqués máximos, donde ${\displaystyle 3a+2b=n}$ y ${\displaystyle b\leq 2}$; cada clique máximo es formado eligiendo un vértice de cada subconjunto de partición. Este es el número más grande de cliqués posibles entre todos los grafos de ${\displaystyle n}$-vértices independientemente del número de aristas en el grafo; estos grafos son varias veces llamados grafos de Moon–Moser.^[4]​

Cada grafo de Turán es un cografo; es decir que puede ser formado a partir de vértices individuales por una secuencia de operaciones de uniones disjuntas y grafos complemento. Específicamente, tal secuencia puede iniciar formando cada uno de los conjuntos independientes de los grafos de Turán como una unión disjunta de vértices aislados. Entonces, el grafo total es el complemento de la unión disjunta de los complementos de esos conjuntos independientes.

Chao y Novacky mostraron en 1982 que los grafos de Turán son cromáticamente únicos: ningún otro grafo tiene los mismos polinomios cromáticos.^[5]​ Nikiforov en 2005 utilizó los grafos de Turán para suplementar un límite menor para la suma del ${\displaystyle k}$-ésimo eigenvector de un grafo y su complemento.^[6]​

Falls, Powell, y Snoeyink desarrollaron un algoritmo eficiente para encontrar racimos de grupos de genes ortólogos en los datos del genoma, representando los datos como un grafo y buscando grandes subgrafos de Turán.^[7]​

Los grafos de Turán también tienen propiedades interesantes relacionadas con la teoría de grafos geométricos. Pór y Wood en 2005 dieron un límite menor de ${\displaystyle \Omega ((rn)^{3/4})}$ en el volumen de cualquier rejilla tridimensional del grafo de Turán.^[8]​ Witsenhausen en 1974 conjetura que la suma máxima de distancias al cuadrado, entre ${\displaystyle n}$ puntos con diámetro unitario en ${\displaystyle R^{d}}$ es alcanzado por una configuración formada al incrustar un grafo de Turán en los vértices de un símplex regular.^[9]​

Un grafo ${\displaystyle G}$ de ${\displaystyle n}$-vértices es el subgrafo de un grafo de Turán ${\displaystyle T(n,r)}$ sí y solo sí ${\displaystyle G}$ admite una coloración equitativa con ${\displaystyle r}$ colores. La partición del grafo de Turán en conjuntos independientes corresponde a la partición de ${\displaystyle G}$ en clases de color. En particular, el grafo de Turán es el único grafo de ${\displaystyle n}$-vértices máximos con una coloración equitativa ${\displaystyle r}$.

• Wikimedia Commons alberga una categoría multimedia sobre Grafo de Turán.
• Weisstein, Eric W. «Grafo de Turán». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Weisstein, Eric W. «Grafo octaédrico». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Weisstein, Eric W. «Grafo de veladas (Cocktail Party Graph)». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.