Función W de Lambert

En matemáticas, la función W de Lambert, denominada así en honor a Johann Heinrich Lambert, si bien también se conoce como función Omega o log producto es la función inversa de f(w) = we^w donde e^w es la función exponencial natural y w es cualquier número complejo. La función se define mediante W. Para todo número complejo denominado z, se tiene:

${\displaystyle z=W(z)e^{W(z)}.}$

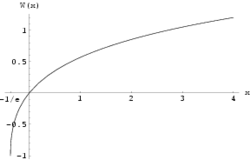
Puesto que la función f no es inyectiva, la función W es multivaluada (excepto en 0). De restringir los argumentos reales, x y w reales, la función es definida solo por x ≥ −1/e, y es doble-valuada en (−1/e, 0); la restricción adicional w ≥ −1 define una función simple-valuada W₀(x), representable gráficamente. Tenemos W₀(0) = 0 y W₀(−1/e) = −1. La rama alternativa en [−1/e, 0) con w ≤ −1 es indicada como W₋₁(x) y decrece de W₋₁(−1/e) = −1 a W₋₁(0⁻) = −∞.

La función W de Lambert no puede expresarse en términos de funciones elementales. Es útil en combinatoria, por ejemplo en la enumeración de árboles. Puede emplearse para resolver varias ecuaciones que alberguen exponenciales y también participa en la solución de ecuaciones diferenciales retrasadas temporalmente, como y'(t) = a y(t − 1).

Definición

Si x es real pero mayor o menor que ${\displaystyle -e^{-1}}$, o si x es complejo o imaginario puro, entonces:

${\displaystyle W(x)={\frac {x}{2\pi }}\int _{-\pi }^{\pi }{\frac {(1-v\cot v)^{2}+v^{2}}{x+v\csc v\cdot e^{-v\cot v}}}{\rm {d}}v\,}$

Si ${\displaystyle {\mathfrak {R}}(x)<-e^{-1},{\mathfrak {I}}(x)\leq -e^{-1}}$，

${\displaystyle W(x)=1+(\ln x-1)e^{-{\frac {\rm {i}}{2\pi }}\int _{0}^{\infty }{\frac {1}{1+t}}\ln {\frac {\ln x+t-\ln t-{\rm {i}}\pi }{\ln x+t-\ln t+{\rm {i}}\pi }}{\rm {d}}t}\,}$

La función ${\displaystyle W_{k}(x)}$ equivale a la siguiente integral:

${\displaystyle W_{k}(x)=1+(\ln x+2k\pi {{\rm {i}}-1)e^{-{\frac {\rm {i}}{2\pi }}\int _{0}^{\infty }{\frac {1}{t+1}}\ln {\frac {\ln x+t-\ln t+(2k-1){\rm {i}}\pi }{\ln x+t-\ln t+(2k+1){\rm {i}}\pi }}{\rm {d}}t}}\,}$

，

donde ${\displaystyle x\in {\mathbb {R} -(-e^{-1};0)},k\in \mathbb {Z} \,}$

Historia

Lambert inicialmente postuló una función relacionada (la ecuación trascendental de Lambert), que dio lugar a un artículo en 1783 en el cual se discutía el caso especial we^w. Sin embargo, la inversa de we^w fue descrita por Polya y Szegö en 1925. La función de Lambert fue "redescubierta" alrededor de una vez por década en aplicaciones especializadas, pero su importancia no se apreció realmente hasta la década de 1990. Cuando se anunció que la función W de Lambert da una solución exacta a los valores propios de la energía del sistema cuántico correspondiente al modelo descrito por el operador de Dirac para duplicar así para el caso de igualdad de cargas - un problema físico fundamental - Corless y los desarrolladores del sistema Maple hicieron una búsqueda bibliográfica y descubrieron que esta función aparece en todas partes en las aplicaciones prácticas.^[1]​

Derivación e integración

Por derivación implícita, se encuentra que W satisface la ecuación diferencial ordinaria.

${\displaystyle z(1+W){\frac {dW}{dz}}=W\quad \mathrm {para\ } z\neq -1/e\,,}$

por lo tanto:

${\displaystyle {\frac {dW}{dz}}={\frac {W(z)}{z(1+W(z))}}\quad \mathrm {para\ } z\neq -1/e\,.}$

La función W (x), y algunas expresiones que implican a W(x), pueden ser integradas empleando la regla de sustitución w = W(x), i.e. x = w e^w:

${\displaystyle \int W(x)\,dx=x\left(W(x)-1+{\frac {1}{W(x)}}\right)+C}$

Series de Taylor

Las series de Taylor de W₀ en torno a 0 pueden ser resueltas mediante el teorema de inversión de Lagrange que procede de:

${\displaystyle \forall |x|<e^{-1}:W_{0}(x)=\sum _{n=1}^{\infty }{\frac {(-n)^{n-1}}{n!}}\ x^{n}=x-x^{2}+{\frac {3}{2}}x^{3}-{\frac {8}{3}}x^{4}+{\frac {125}{24}}x^{5}-\cdots }$

El radio de convergencia es 1/e, como puede verse mediante el criterio de d'Alembert. La función definida por las series puede extenderse a una función holomórfica definida para todos los números complejos con un corte de rama en torno al intervalo (−∞, −1/e]; la mencionada función holomórfica define la rama principal de la función W de Lambert.

Aplicaciones

Algunas ecuaciones que poseen exponenciales pueden resolverse mediante esta función. Para ello, la estrategia general consiste en sustituir todas las instancias de lo desconocido a una parte de la ecuación y tornarla, entonces, a la forma Y = Xe^X, para la cual W proporciona una solución.

Es decir:

${\displaystyle X=Ye^{Y}\;\Longleftrightarrow \;Y=W(X)}$

Ejemplos

Ejemplo 1

${\displaystyle 2^{t}=5t\,}$

${\displaystyle \Rightarrow 1={\frac {5t}{2^{t}}}\,}$

${\displaystyle \Rightarrow 1=5t\,e^{-t\ln 2}\,}$

${\displaystyle \Rightarrow {\frac {1}{5}}=t\,e^{-t\ln 2}\,}$

${\displaystyle \Rightarrow {\frac {-\,\ln 2}{5}}=(-\,t\,\ln 2)\,e^{(-t\ln 2)}\,}$

${\displaystyle \Rightarrow -t\ln 2=W\left({\frac {-\ln 2}{5}}\right)\,}$

${\displaystyle \Rightarrow t={\frac {-W\left({\frac {-\ln 2}{5}}\right)}{\ln 2}}\,}$

De forma más general, la ecuación

${\displaystyle ~p^{ax+b}=cx+d}$

donde

${\displaystyle p>0\land c,d\neq 0}$

puede transformarse mediante la sustitución

${\displaystyle -t=ax+{\frac {ad}{c}}}$

en

${\displaystyle tp^{t}=R=-{\frac {a}{c}}p^{b-{\frac {ad}{c}}}}$

dando

${\displaystyle t={\frac {W(R\ln p)}{\ln p}}}$

que se resuelve como

${\displaystyle x=-{\frac {W(-{\frac {a\ln p}{c}}\,p^{b-{\frac {ad}{c}}})}{a\ln p}}-{\frac {d}{c}}}$

Ejemplo 2

Técnicas similares llevan a

${\displaystyle x^{x}=z\,,}$

con solución

${\displaystyle x={\frac {\ln(z)}{W(\ln z)}}\,,}$

o, de forma equivalente,

${\displaystyle x=\exp \left(W(\ln(z))\right).}$

Ejemplo 3

Siempre que el exponencial complejo infinito tipo tetración

${\displaystyle z^{z^{z^{\cdot ^{\cdot ^{\cdot }}}}}\!}$

converja, la función W de Lambert proporciona un valor límite como

${\displaystyle c={\frac {W(-\ln(z))}{-\ln(z)}}}$

en el cual ln(z) denota la rama principal de la función logarítmica compleja.

Ejemplo 4

Las soluciones para

${\displaystyle x\log _{b}\left(x\right)=a}$

poseen la forma

${\displaystyle x={\frac {a\ln(b)}{W(a\ln(b))}}}$

Ejemplo 5

${\displaystyle a^{x}=bx^{c}}$

donde ${\displaystyle a>0\ ,\neq 1\land b,c\neq 0}$

${\displaystyle \Rightarrow a^{x/c}=b^{1/c}\ x}$

${\displaystyle \Rightarrow 1={\frac {b^{1/c}\ x}{a^{x/c}}}}$

${\displaystyle \Rightarrow 1=b^{1/c}\ x\ e^{-(x/c)\ln(a)}}$

${\displaystyle \Rightarrow {\frac {1}{b^{1/c}}}=x\ e^{-(x/c)\ln(a)}}$

${\displaystyle \Rightarrow -{\frac {\ln(a)}{c\ b^{1/c}}}=-(x/c)\ln(a)\ e^{-(x/c)\ln(a)}}$

${\displaystyle \Rightarrow W\left(-{\frac {\ln(a)}{c\ b^{1/c}}}\right)=-(x/c)\ln(a)}$

${\displaystyle \Rightarrow x=-{\frac {c}{\ln(a)}}W\left(-{\frac {\ln(a)}{c\ b^{1/c}}}\right)}$

Ejemplo 6

La solución para la corriente eléctrica en circuitos diodo/resistencia puede escribirse como una función W.

Ejemplo 7

La ecuación diferencial con retardo

${\displaystyle {\dot {y}}(t)=ay(t-1)}$

posee la ecuación característica ${\displaystyle \lambda =ae^{-\lambda }}$, que lleva a ${\displaystyle \lambda =W_{k}(a)}$ y ${\displaystyle y(t)=e^{W_{k}(a)t}}$, donde ${\displaystyle k}$ es el índice de la rama. Si ${\displaystyle a}$ es real, sólo debe considerarse ${\displaystyle W_{0}(a)}$.

Generalizaciones

La función W de Lambert abastece de soluciones reales a las ecuaciones "algébricas-transcendentales" (de eso x) de la forma:

${\displaystyle e^{-cx}=a_{o}(x-r)~~\quad \qquad \qquad \qquad \qquad (1)}$

o a₀, c y r son constantes reales. La solución es ${\displaystyle x=r+W(ce^{-cr}/a_{o})/c}$. Las generalizaciones de la función W de Lambert^[2]​^[3]​^[4]​ incluye:

• un lazo antaño desconocido entre la Relatividad general y la Mecánica cuántica (Gravedad cuántica) en dimensiones reducidas, y descrito en el periódico Classical and Quantum Gravity (la gravita clásica y cuántica)^[5]​ o la parte(partida) de derecha de la ecuación (1) es ahora un polinomio cuadrático x:

${\displaystyle e^{-cx}=a_{o}(x-r_{1})(x-r_{2})~~\qquad \qquad (2)}$

o r₁ y r₂ son unas constantes reales, las raíces del polinomio cuadrático. En este caso, la solución es una función con un solo argumento x pero los términos como r_i y a_o son unos parámetros de la función. De este punto de vista, la generalización se parece a la Serie hipergeométrica y la función de Meijer G pero pertenece sin embargo a una "clase" diferente de funciones. Cuando r₁ = r₂, cada lado de (2) puede ser factorizado y se reduce a (1) y pues la solución se reduce a la de la función estándar de W. La ecuación (2) es la gobernante el campo de un Dilatón - por el cual es derivada la métrica del sistema gravitacional de dos cuerpos en las dimensiones 1+1 (es decir una dimensión espacial y una dimensión temporal) para el caso de las masas (al descanso) desiguales - así como los valores limpios de la energía del sistema cuántico que consiste del modelo descrito por el operador de Dirac a pozo doble para el caso de cargas(gastos) desiguales en una dimensión.

• las soluciones analíticas para los valores limpios de la energía de un caso especial de la versión cuántica del problema de los tres cuerpos, es decir el ion hidrogena molecular (en tres dimensiones).^[6]​ La parte de derecha de (1) (o (2)) es ahora un cociente de polinomios de orden infinita x:

${\displaystyle e^{-cx}=a_{o}{\frac {\prod _{i=1}^{\infty }(x-r_{i})}{\prod _{i=1}^{\infty }(x-s_{i})}}\qquad \qquad \qquad (3)}$

O r_i y s_i son constantes reales distintas y x es una función del valor limpio de la energía y la distancia internuclear R. La ecuación (3) con estos casos especializados y exprimidos(expresados) en (1) y (2) corresponde a una clase considerable de ecuaciones a plazo diferencial. Gracias por la noción de Hardy de un "falso derivativo", múltiples raíces exactas se han encontrado en casos especiales de ecuación (3).^[7]​

Las aplicaciones de la función W de Lambert en los problemas de la física fundamental hasta no son agotadas para el caso estándar exprimido en (1), como se ve en física atómica y molecular^[8]​ y el criterio de Keiper-Li para la Hipótesis de Riemann. ^[9]​

Valores especiales

${\displaystyle W\left(-{\frac {\pi }{2}}\right)={\frac {i\pi }{2}}}$

${\displaystyle W\left(-{\frac {\ln 2}{2}}\right)=-\ln 2}$

${\displaystyle W\left(-{1 \over e}\right)=-1}$

${\displaystyle W(0)=0\,}$

${\displaystyle W(1)=\Omega \,}$ (la Constante Omega de Lambert)

${\displaystyle W(e)=1\,}$

Algoritmo de evaluación

La función W puede evaluarse mediante la relación de recurrencia

${\displaystyle w_{j+1}=w_{j}-{\frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}(w_{j}+1)-{\frac {(w_{j}+2)(w_{j}e^{w_{j}}-z)}{2w_{j}+2}}}}}$

proporcionada en Corless et al. para calcular W. Junto con la estima de evaluación de error de Chapeau-Blondeau y Monir. Esto calcula la rama principal para ${\displaystyle x>-1/e}$.

Gráficos

• Representaciones de la función W de Lambert en el plano complejo
• 
  z = Re(W₀(x + i y))
• 
  z = Im(W₀(x + i y))
• 
  W₀(x + i y)
• 

Notas

Referencias y enlaces externos

• Weisstein, Eric W. «Lambert W-Function». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Lambert function from Wolfram's function site.
• Computing the Lambert Wfunction
• Corless et al. Notes about Lambert W research
• Corless et al. "On the Lambert W function" Adv. Computational Maths. 5, 329 - 359 (1996) (PDF)
• Chapeau-Blondeau, F. and Monir, A: "Evaluation of the Lambert W Function and Application to Generation of Generalized Gaussian Noise With Exponent 1/2", IEEE Trans. Signal Processing, 50(9), 2002
• Francis et al. "Quantitative General Theory for Periodic Breathing" Circulation 102 (18): 2214. (2000). Use of Lambert function to solve delay-differential dynamics in human disease.
• Extreme Mathematics. Monographs on the Lambert W function, its numerical approximation and generalizations for W-like inverses of transcendental forms with repeated exponential towers.
• Código en C