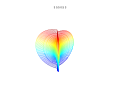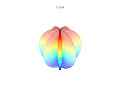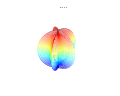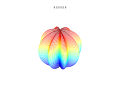Superformula
The superformula is a generalization of the superellipse and was proposed by Johan Gielis around 2000.[1] Gielis suggested that the formula can be used to describe many complex shapes and curves that are found in nature. Gielis has filed a patent application related to the synthesis of patterns generated by the superformula, which expired effective 2020-05-10.[2]
In polar coordinates, with the radius and the angle, the superformula is:
By choosing different values for the parameters and different shapes can be generated.
The formula was obtained by generalizing the superellipse, named and popularized by Piet Hein, a Danish mathematician.
2D plots
In the following examples the values shown above each figure should be m, n1, n2 and n3.

A GNU Octave program for generating these figures
function sf2d(n, a) u = [0:.001:2 * pi]; raux = abs(1 / a(1) .* abs(cos(n(1) * u / 4))) .^ n(3) + abs(1 / a(2) .* abs(sin(n(1) * u / 4))) .^ n(4); r = abs(raux) .^ (- 1 / n(2)); x = r .* cos(u); y = r .* sin(u); plot(x, y); end
Extension to higher dimensions
It is possible to extend the formula to 3, 4, or n dimensions, by means of the spherical product of superformulas. For example, the 3D parametric surface is obtained by multiplying two superformulas r1 and r2. The coordinates are defined by the relations:
where (latitude) varies between −π/2 and π/2 and θ (longitude) between −π and π.
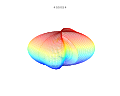
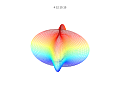
3D plots
3D superformula: a = b = 1; m, n1, n2 and n3 are shown in the pictures.
A GNU Octave program for generating these figures:
function sf3d(n, a) u = [- pi:.05:pi]; v = [- pi / 2:.05:pi / 2]; nu = length(u); nv = length(v); for i = 1:nu for j = 1:nv raux1 = abs(1 / a(1) * abs(cos(n(1) .* u(i) / 4))) .^ n(3) + abs(1 / a(2) * abs(sin(n(1) * u(i) / 4))) .^ n(4); r1 = abs(raux1) .^ (- 1 / n(2)); raux2 = abs(1 / a(1) * abs(cos(n(1) * v(j) / 4))) .^ n(3) + abs(1 / a(2) * abs(sin(n(1) * v(j) / 4))) .^ n(4); r2 = abs(raux2) .^ (- 1 / n(2)); x(i, j) = r1 * cos(u(i)) * r2 * cos(v(j)); y(i, j) = r1 * sin(u(i)) * r2 * cos(v(j)); z(i, j) = r2 * sin(v(j)); endfor; endfor; mesh(x, y, z); endfunction;
Generalization
The superformula can be generalized by allowing distinct m parameters in the two terms of the superformula. By replacing the first parameter with y and second parameter with z:[3]
This allows the creation of rotationally asymmetric and nested structures. In the following examples a, b, and are 1:

References
- ^ Gielis, Johan (2003), "A generic geometric transformation that unifies a wide range of natural and abstract shapes", American Journal of Botany, 90 (3): 333–338, doi:10.3732/ajb.90.3.333, ISSN 0002-9122, PMID 21659124

- ^ EP patent 1177529, Gielis, Johan, "Method and apparatus for synthesizing patterns", issued 2005-02-02
- ^ * Stöhr, Uwe (2004), SuperformulaU (PDF), archived from the original (PDF) on December 8, 2017
External links

- Some Experiments on Fitting of Gielis Curves by Simulated Annealing and Particle Swarm Methods of Global Optimization
- Least Squares Fitting of Chacón-Gielis Curves By the Particle Swarm Method of Optimization
- Superformula 2D Plotter & SVG Generator
- Interactive example using JSXGraph
- SuperShaper: An OpenSource, OpenCL accelerated, interactive 3D SuperShape generator with shader based visualisation (OpenGL3)