Umlaufzahl (Mathematik)

Die Umlaufzahl (auch Windungszahl oder Index genannt) ist eine topologische Invariante, die eine entscheidende Rolle in der Funktionentheorie spielt.

Die Umlaufzahl einer Kurve ${\displaystyle \gamma }$ in Bezug auf einen Punkt ${\displaystyle z_{0}}$ stellt die Anzahl der Umrundungen entgegen der Uhrzeigerrichtung um ${\displaystyle z_{0}}$ dar, wenn man dem Verlauf der Kurve folgt. Eine Umrundung in Uhrzeigerrichtung ergibt die negative Windungszahl −1.

Windungszahl

1	−1	0	1	2

Ist ${\displaystyle \gamma }$ eine geschlossene Kurve in ${\displaystyle \mathbb {C} }$ und ist ferner ${\displaystyle z_{0}}$ ein Punkt in ${\displaystyle \mathbb {C} ,}$ der nicht auf ${\displaystyle \gamma }$ liegt, dann ist die Umlaufzahl von ${\displaystyle \gamma }$ in Bezug auf ${\displaystyle z_{0}}$ so definiert:

${\displaystyle \operatorname {ind} _{\gamma }(z_{0})=n(\gamma ,z_{0}):={\frac {1}{2\pi \mathrm {i} }}\int _{\gamma }{\frac {\mathrm {d} \zeta }{\zeta -z_{0}}}}$

Die Umlaufzahl ${\displaystyle \operatorname {ind} }$ (nach dem englischen index) wird in der Literatur oft auch mit ${\displaystyle I}$ oder ${\displaystyle \chi }$ bezeichnet. Die Umlaufzahl einer geschlossenen Kurve ist unabhängig vom Bezugspunkt immer eine ganze Zahl.

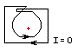
Intuitiv lässt sich die Windungszahl mittels

${\displaystyle \operatorname {ind} _{\gamma }(z_{0})=}$ (Anzahl der Umläufe von ${\displaystyle \gamma }$ um ${\displaystyle z_{0}}$ entgegen dem Uhrzeigersinn) − (Anzahl der Umläufe von ${\displaystyle \gamma }$ um ${\displaystyle z_{0}}$ im Uhrzeigersinn)

berechnen. Die Berechnung über die Definition ist oft nicht ohne Weiteres möglich. Als Beispiel wählen wir den Einheitskreis

${\displaystyle \gamma \colon [0,2\pi ]\to \mathbb {C} ,\,t\mapsto e^{\mathrm {i} t}}$

als Kurve. Nach der intuitiven Regel ist ${\displaystyle \operatorname {ind} _{\gamma }(z)=1}$ für alle Punkte ${\displaystyle z\in \mathbb {E} }$ in seinem Inneren ${\displaystyle \mathbb {E} }$ und ${\displaystyle \operatorname {ind} _{\gamma }(z)=0}$ für alle Punkte ${\displaystyle z\in \mathbb {C} \setminus {\bar {\mathbb {E} }}}$ außerhalb der abgeschlossenen Kreisscheibe ${\displaystyle {\bar {\mathbb {E} }}}$. Letzteres folgt sofort aus dem Integralsatz von Cauchy und der Definition. Sei nun

${\displaystyle f\colon \mathbb {E} \to \mathbb {C} ,\,z\mapsto \operatorname {ind} _{\gamma }(z).}$

Es gilt

${\displaystyle \operatorname {ind} _{\gamma }(0)=f(0)={\frac {1}{2\pi \mathrm {i} }}\int _{\gamma }{\frac {\mathrm {d} \zeta }{\zeta }}={\frac {1}{2\pi \mathrm {i} }}\int \limits _{0}^{2\pi }{\frac {\mathrm {i} e^{\mathrm {i} t}}{e^{\mathrm {i} t}}}\mathrm {d} t=1.}$

Durch Vertauschen von Differentiation und Integration ergibt sich

${\displaystyle f'(z)={\frac {1}{2\pi \mathrm {i} }}\int _{\gamma }{\frac {\mathrm {d} \zeta }{\left(\zeta -z\right)^{2}}}}$,

und weil ${\displaystyle \zeta \mapsto -{\frac {1}{\zeta -z}}}$ eine Stammfunktion des Integranden ist, ist ${\displaystyle f'\equiv 0.}$ Weil ${\displaystyle \mathbb {E} }$ zusammenhängend ist, ist also ${\displaystyle f(z)=\operatorname {ind} _{\gamma }(z)=1}$ für alle ${\displaystyle z\in \mathbb {E} .}$

Die Umlaufzahl wird vor allem bei der Berechnung von Kurvenintegralen in der komplexen Zahlenebene verwendet. Sei

${\displaystyle f\colon \mathbb {C} \setminus \left\{a_{1},\dotsc ,a_{n}\right\}\to \mathbb {C} }$

eine meromorphe Funktion mit Singularitäten ${\displaystyle a_{1},\dotsc ,a_{n},}$ dann kann man nach dem Residuensatz das Integral von ${\displaystyle f}$ über eine (durch keine der Singularitäten verlaufende) Kurve ${\displaystyle \gamma }$ durch

${\displaystyle \int _{\gamma }f=2\pi \mathrm {i} \sum _{k=1}^{n}\operatorname {ind} _{\gamma }(a_{k})\operatorname {Res} _{a_{k}}f}$

berechnen.

In der algorithmischen Geometrie wird die Umlaufzahl verwendet, um zu bestimmen, ob ein Punkt außerhalb oder innerhalb eines nichteinfachen Polygons (eines Polygons, dessen Kanten sich überschneiden) liegt. Für einfache Polygone vereinfacht sich der Algorithmus zur Even-Odd-Regel.

Für Polygone (geschlossene Kantenzüge) verwendet man zur Berechnung der Umlaufzahl folgenden Algorithmus:

1. Suche eine Halbgerade (beginnend beim zu untersuchenden Punkt nach außen), die keine Eckpunkte des Polygons enthält.
2. Setze ${\displaystyle w=0.}$
3. Für alle Schnittpunkte der Halbgerade mit dem Polygonzug:
   • Schneidet die Halbgerade eine Polygonkante, die „von rechts nach links“ orientiert ist (wenn der Punkt auf der linken Seite der Kante liegt), erhöhe ${\displaystyle w}$ um 1.
   • Schneidet die Halbgerade eine Polygonkante, die „von links nach rechts“ orientiert ist (wenn der Punkt auf der rechten Seite der Kante liegt), verkleinere ${\displaystyle w}$ um 1.
4. ${\displaystyle w}$ ist nun die Umlaufzahl des Punktes.

Ist die Umlaufzahl 0, so liegt der Punkt außerhalb des Polygons, sonst innerhalb.

In nebenstehendem Beispiel ist die Halbgerade, mit der gestartet wird, der senkrechte Pfeil. Er schneidet drei Kanten des Polygons. Bezüglich der roten Kante liegt der Punkt rechts ${\displaystyle \left(w=-1\right).}$ Bezüglich der nächsten Kante liegt der Punkt auch rechts ${\displaystyle \left(w=-2\right)}$ und bzgl. der letzten Kante liegt der Punkt links ${\displaystyle \left(w=-1\right).}$ Der Punkt liegt innerhalb des Polygons. Die Polygonfläche ist grau hinterlegt.

Ein analoger Algorithmus ergibt auch für nicht geradlinig verlaufende (geschlossene) Kurven die Umlaufzahl um einen Punkt, allerdings ist da das Überprüfen der Schnittpunkte nicht so einfach zu implementieren.

Eine Verallgemeinerung für ${\displaystyle n}$-dimensionale Mannigfaltigkeiten stammt von Nikolai Nikolajewitsch Bogoljubow: Unter Benutzung des allgemeinen Stokes’schen Satzes für ${\displaystyle z_{0}=0}$ kann man

${\displaystyle \mathrm {ind} _{\gamma }(0)={\frac {1}{n\mathrm {Vol(B)} }}\oint _{\gamma }{\frac {{\vec {x}}\cdot \mathrm {d} {\vec {S}}}{\|x\|^{n}}}}$

schreiben. ${\displaystyle B}$ ist die Einheitskugel im ${\displaystyle \mathbb {R} ^{n},}$ ${\displaystyle \gamma }$ ist die betrachtete ${\displaystyle (n-1)}$-dimensionale geschlossene Mannigfaltigkeit, auf der integriert werden soll.

• Cauchysche Integralformel
• Residuensatz
• Kurvenintegral

• Eberhard Freitag, Rolf Busam: Funktionentheorie 1. Springer-Verlag, Berlin, ISBN 3-540-67641-4.