Impulsinvarianz-Transformation

Die Impulsinvarianz-Transformation (Impulsinvariante-Transformation, IIR) ist ein mathematisches Verfahren (eine systemantwortinvariante Transformation) und dient zur Synthese zeitdiskreter, hauptsächlich digitaler Filter.

Hierfür wird die Impulsantwort eines analogen Filters ${\displaystyle g_{a}(t)}$ durch äquidistante Abtastung in die zeitdiskrete Impulsantwort ${\displaystyle g(k)}$ mit ${\displaystyle g(k)=g_{a}(kT)}$ überführt. Die Impulsantwort des zeitdiskreten Filters stimmt somit an den Abtastzeitpunkten ${\displaystyle kT}$ mit der Impulsantwort des analogen Filters überein.

Um die impulsinvariante Transformation nun durchzuführen, geht man wie folgt vor. Mittels inverser Laplace-Transformation erhält man die Impulsantwort ${\displaystyle g_{a}(t)}$ aus der Übertragungsfunktion ${\displaystyle G(s)}$ des analogen Filters:

${\displaystyle g_{a}(t)=L^{-1}\left\{G(s)\right\}}$

Um die Impulsantwort nun "abzutasten", substituiert man ${\displaystyle t}$ durch ${\displaystyle kT}$ in ${\displaystyle g_{a}(t)}$. Hierbei sei ${\displaystyle T}$ die Abtastperiode. Die z-Übertragungsfunktion erhält man nun aus der abgetasteten Impulsantwort mit Hilfe der z-Transformation. Zusammengefasst lässt sich die impulsinvariante Transformation also als

${\displaystyle G(z)=T\cdot Z\left\{\left.L^{-1}\left\{G(s)\right\}\right|_{t=k\,T}\right\}}$

schreiben. Durch die Multiplikation mit ${\displaystyle T}$ kürzt sich der Vorfaktor ${\displaystyle {\frac {1}{T}}}$ des Spektrum des abgetasteten Signals, so dass das Spektrum des abgetasteten Signals (bis auf Aliasing) unabhängig von der Abtastperiode wird.

Hierdurch kann ein zeitdiskretes Filter entworfen werden, welches an den Abtastzeitpunkten ${\displaystyle kT}$ die gleiche Impulsantwort hat wie ein entsprechendes analoges Filter. Dies macht sich bei geeignet hoher Abtastung im Frequenzbereich kaum bemerkbar. Das zeitdiskrete Filter approximiert somit den Frequenzgang des analogen Filters.

Mit der Transformation

${\displaystyle G(z)=\left(1-z^{-1}\right)\cdot Z\left\{\left.L^{-1}\left\{{\frac {G(s)}{s}}\right\}\right|_{t=k\,T}\right\}}$

würde man eine z-Übertragungsfunktion erhalten, die an den Abtastzeitpunkten ${\displaystyle kT}$ die gleiche Sprungantwort aufweist.

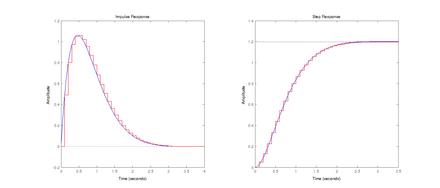
Gegeben sei ein analoges Filter mit der folgenden Übertragungsfunktion:

${\displaystyle G(s)={\frac {6}{s^{2}+4s+5}}}$

Die Impulsantwort des Filters lautet:

${\displaystyle L^{-1}\left\{G(s)\right\}=6\mathrm {e} ^{-2t}\sin t}$

Wir substituieren nun ${\displaystyle t}$ durch ${\displaystyle kT}$, womit wir

${\displaystyle 6\mathrm {e} ^{-2kT}\sin kT}$

erhalten. Die z-Transformierte von ${\displaystyle \sin kT}$ lautet ${\displaystyle {\frac {z\sin T}{z^{2}-2z\cos T+1}}}$. Der Vorfaktor ${\displaystyle \mathrm {e} ^{-2kT}}$ lässt sich als ${\displaystyle a^{-k}=\left(\mathrm {e} ^{2T}\right)^{-k}}$ schreiben; unter Anwendung des Dämpfungssatzes der z-Transformation, der da lautet ${\displaystyle Z\left\{a^{-k}x[k]\right\}=X(az)}$ erhält man somit

${\displaystyle G(z)=6T\cdot {\frac {az\sin T}{a^{2}z^{2}-2az\cos T+1}}}$

für die diskretisierte Übertragungsfunktion des Filters. Zum Vergleich der Impulsantwort bzw. der Sprungantwort des analogen und des diskretisierten Filters siehe nebenstehendes Bild.

• Hermann Götz: Einführung in die digitale Signalverarbeitung. 3. überarbeitete und erweiterte Auflage. Teubner, Stuttgart u. a. 1998, ISBN 3-519-20117-8, (Teubner-Studienskripten 117 Elektrotechnik).
• Alan V. Oppenheim, Ronald W. Schafer: Zeitdiskrete Signalverarbeitung. 3. durchgesehene Auflage. Oldenbourg, München u. a. 1999, ISBN 3-486-22948-6.