Faktorraum

Der Quotientenvektorraum, auch kurz Quotientenraum oder Faktorraum genannt, ist ein Begriff aus der linearen Algebra, einem Teilgebiet der Mathematik. Er ist derjenige Vektorraum, der als Bild einer Parallelprojektion entlang eines Untervektorraums entsteht. Die Elemente des Quotientenvektorraumes sind Äquivalenzklassen.

Es sei ${\displaystyle V}$ ein Vektorraum über einem Körper ${\displaystyle K}$ und ${\displaystyle U}$ ein Untervektorraum von ${\displaystyle V}$. Durch die Festsetzung

${\displaystyle v_{1}\sim v_{2}\;:\!\iff v_{1}-v_{2}\in U}$ für ${\displaystyle v_{1},v_{2}\in V}$

wird auf ${\displaystyle V}$ eine Äquivalenzrelation definiert.

Die Vektoren ${\displaystyle v_{1}}$ und ${\displaystyle v_{2}}$ sind also äquivalent, wenn sie sich um einen Vektor aus ${\displaystyle U}$ unterscheiden. Anders gesagt: Wenn die Gerade durch die Punkte ${\displaystyle v_{1}}$ und ${\displaystyle v_{2}}$ parallel zu ${\displaystyle U}$ ist, sind ${\displaystyle v_{1}}$ und ${\displaystyle v_{2}}$ äquivalent.

Die Äquivalenzklasse eines Vektors ${\displaystyle v}$ ist

${\displaystyle [v]:=v+U:=\{v+u\mid u\in U\}}$,

anschaulich der zu ${\displaystyle U}$ „parallele“ affine Unterraum durch ${\displaystyle v}$. Die Äquivalenzklassen werden auch als Nebenklassen bezeichnet (dieser Begriff stammt aus der Gruppentheorie).

Der Quotientenvektorraum von ${\displaystyle V}$ nach ${\displaystyle U}$ ist die Menge aller Äquivalenzklassen und wird mit ${\displaystyle V/U}$ bezeichnet:

${\displaystyle V/U:=\{[v]\mid v\in V\}}$.

Er bildet einen Vektorraum, wenn die Vektorraumoperationen vertreterweise definiert werden:

• ${\displaystyle [v_{1}]+[v_{2}]=[v_{1}+v_{2}]}$
• ${\displaystyle \lambda \cdot [v]=[\lambda v]}$

für ${\displaystyle v,v_{1},v_{2}\in V}$ und ${\displaystyle \lambda \in K}$.

Diese Operationen sind wohldefiniert, also von der Wahl der Vertreter unabhängig.

• Es gibt eine kanonische surjektive lineare Abbildung

${\displaystyle \pi \colon \;V\to V/U,\;v\mapsto [v]}$.

• Ist ${\displaystyle W}$ ein Komplement von ${\displaystyle U}$ in ${\displaystyle V}$, d. h. ist ${\displaystyle V}$ die direkte Summe von ${\displaystyle U}$ und ${\displaystyle W}$, so ist die Einschränkung von ${\displaystyle \pi }$ auf ${\displaystyle W}$ ein Isomorphismus. Es gibt aber keine kanonische Möglichkeit, ${\displaystyle V/U}$ als Unterraum von ${\displaystyle V}$ aufzufassen.

• Ist ${\displaystyle V}$ endlichdimensional, dann ergibt sich daraus die folgende Beziehung für die Dimensionen:

${\displaystyle \dim U+\dim V/U=\dim V}$

• Der Dualraum von ${\displaystyle V/U}$ kann mit denjenigen Linearformen auf ${\displaystyle V}$ identifiziert werden, die auf ${\displaystyle U}$ identisch ${\displaystyle 0}$ sind.

• Der Homomorphiesatz besagt, dass eine lineare Abbildung ${\displaystyle f\colon \;V\to W}$ einen Isomorphismus

${\displaystyle V/(\ker f)\to \mathrm {im} \,f}$

zwischen dem Quotientenraum von ${\displaystyle V}$ nach dem Kern von ${\displaystyle f}$ und dem Bild von ${\displaystyle f}$ induziert, d. h. die Verkettung

${\displaystyle V\longrightarrow V/(\ker f)\longrightarrow \mathrm {im} \,f\longrightarrow W}$

ist gleich ${\displaystyle f}$.

Viele normierte Räume entstehen auf die folgende Weise: Sei ${\displaystyle V}$ ein reeller oder komplexer Vektorraum und sei ${\displaystyle p}$ eine Halbnorm auf ${\displaystyle V}$. Dann ist ${\displaystyle U=\{v\in V\mid p(v)=0\}}$ ein Untervektorraum von ${\displaystyle V}$. Der Quotientenraum ${\displaystyle V/U}$ wird dann mit der Norm ${\displaystyle [v]\mapsto p(v)}$ ein normierter Vektorraum.

Allgemeiner: Sei ${\displaystyle V}$ ein topologischer Vektorraum, der nicht hausdorffsch ist. Dann lässt sich analog zu oben ein Unterraum definieren: ${\displaystyle U=\{v\in V\mid {\text{Jede }}0{\text{-Umgebung enthält }}v\}={\overline {\{0\}}}}$. Der Quotientenraum ${\displaystyle V/U}$ wird mit der Quotiententopologie ein hausdorffscher topologischer Vektorraum.

Die ${\displaystyle L^{p}}$-Räume und damit auch die Sobolew-Räume sind Quotientenvektorräume.

Gegeben sei der Vektorraum ${\displaystyle V=\mathbb {R} ^{2}}$ und der eindimensionale Untervektorraum ${\displaystyle U=\left\{\left.{\bigl (}{\begin{smallmatrix}x\\x\end{smallmatrix}}{\bigr )}\right|x\in \mathbb {R} \right\}}$. Dann ist zum Beispiel

${\displaystyle {\bigl (}{\begin{smallmatrix}42\\12\end{smallmatrix}}{\bigr )}+U:=\left\{\left.{\bigl (}{\begin{smallmatrix}42\\12\end{smallmatrix}}{\bigr )}+u\,\right|u\in U\right\}}$

eine Äquivalenzklasse des Quotientenraumes ${\displaystyle V/U}$.

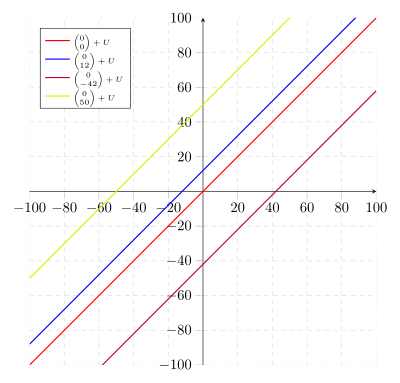
Anschaulich ist jede Gerade, die parallel zur winkelhalbierenden Gerade des 1. Quadranten ist, eine Äquivalenzklasse:

• Quotientenabbildung
• Quotientenmodul

• Gerd Fischer: Lineare Algebra. Vieweg-Verlag, ISBN 3-528-97217-3.
• Klaus Jänich: Lineare Algebra. Springer-Lehrbuch, ISBN 3-540-66888-8.