Funció de Green

En matemàtiques, una funció de Green és la resposta a l'impuls d'un operador diferencial lineal no homogeni definit en un domini amb condicions inicials o condicions de contorn especificades.

Això vol dir que si L és l'operador diferencial lineal, aleshores

• la funció de Green G és la solució de l'equació LG = δ, on δ és la funció delta de Dirac;
• la solució del problema de valor inicial Ly = f és la convolució (G ⁎ f), on G és la funció de Green.

Mitjançant el principi de superposició, donada una equació diferencial ordinària lineal (EDO), L(solució) = font, primer es pot resoldre L(verd) = δs, per a cada s, i adonant-se que, ja que la font és una suma de funcions delta, la solució també és una suma de les funcions de Green, per linealitat de L.

• 
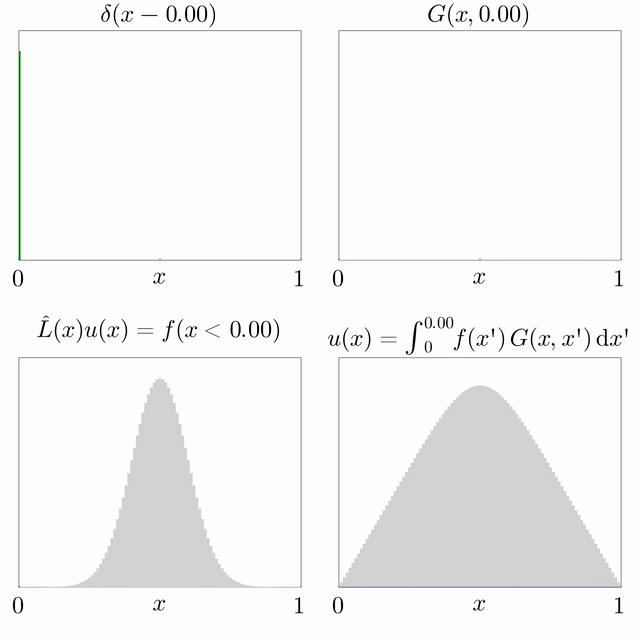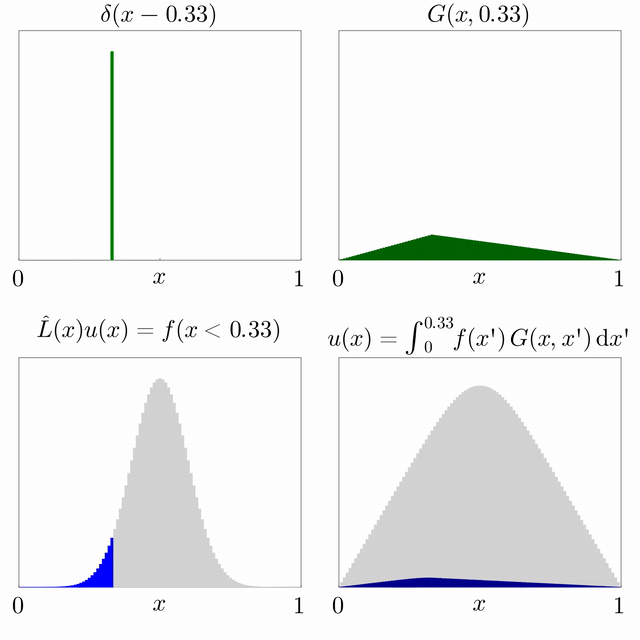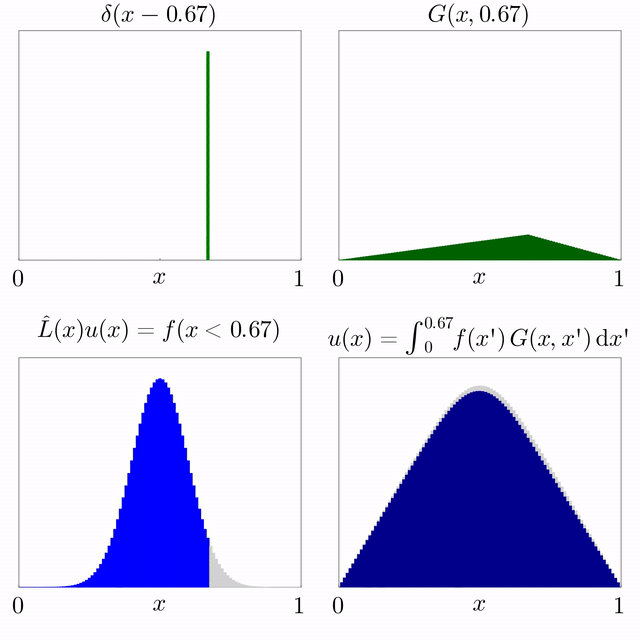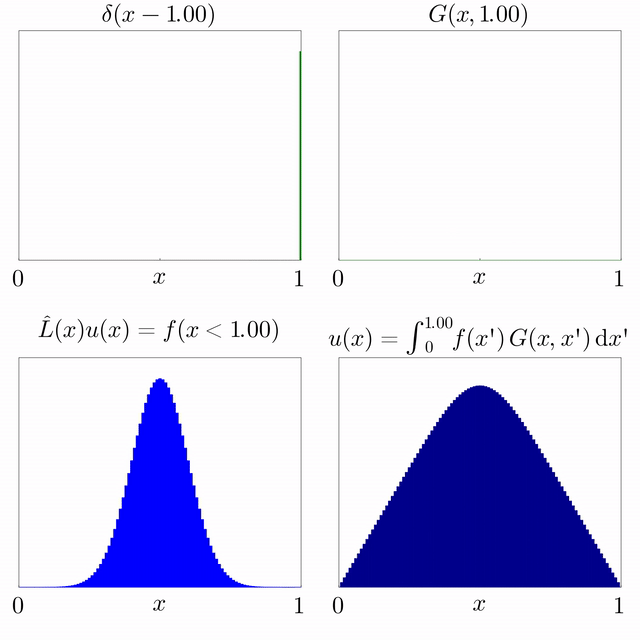  Si es coneix la solució d'una equació diferencial subjecta a una font puntual ${\textstyle {\hat {L}}(x)G(x,y)=\delta (x-y)}$ i l'operador diferencial ${\textstyle {\hat {L}}(x)}$ és lineal, llavors es pot superposar per trobar la solució ${\textstyle u(x)=\int f(y)G(x,y)\,dy}$ per a una font general ${\textstyle {\hat {L}}(x)u(x)=f(x)}$

Les funcions de Green reben el nom del matemàtic britànic George Green, que va desenvolupar el concepte per primera vegada a la dècada del 1820. En l'estudi modern de les equacions diferencials en derivades parcials lineals, les funcions de Green s'estudien en gran part des del punt de vista de les solucions fonamentals.

Sota la teoria de molts cossos, el terme també s'utilitza en física, específicament en teoria quàntica de camps, aerodinàmica, aeroacústica, electrodinàmica, sismologia i teoria estadística de camps, per referir-se a diversos tipus de funcions de correlació, fins i tot aquelles que no s'ajusten a la definició matemàtica. En la teoria quàntica de camps, les funcions de Green prenen el paper de propagadors.

Una funció de Green, G(x,s), d'un operador diferencial lineal ${\displaystyle \operatorname {L} =\operatorname {L} (x)}$ actuant sobre distribucions sobre un subconjunt de l'espai euclidià ${\displaystyle \mathbb {R} ^{n}}$, en un punt s, és qualsevol solució de

on δ és la funció delta de Dirac. Aquesta propietat de la funció de Green es pot aprofitar per resoldre equacions diferencials de la forma

Si el nucli de L no és trivial, aleshores la funció de Green no és única. Tanmateix, a la pràctica, alguna combinació de simetria, condicions de contorn i/o altres criteris imposats externament donaran una funció única de Green. Les funcions de Green es poden classificar, segons el tipus de condicions de contorn satisfetes, pel nombre de la funció de Green. A més, les funcions de Green en general són distribucions, no necessàriament funcions d'una variable real.

Les funcions de Green també són eines útils per resoldre equacions d'ona i equacions de difusió. En mecànica quàntica, la funció de Green del Hamiltonià és un concepte clau amb vincles importants amb el concepte de densitat d'estats.

La funció de Green tal com s'utilitza a la física es defineix normalment amb el signe oposat. És a dir,

$${\displaystyle \operatorname {L} \,G(x,s)=\delta (x-s)~.}$$

Aquesta definició no canvia significativament cap de les propietats de la funció de Green a causa de la uniformitat de la funció delta de Dirac.

Si l'operador és invariant de translació, és a dir, quan ${\displaystyle \operatorname {L} }$ té coeficients constants respecte a x, llavors la funció de Green es pot considerar un nucli de convolució, és a dir,

$${\displaystyle G(x,s)=G(x-s)~.}$$

En aquest cas, la funció de Green és la mateixa que la resposta d'impuls de la teoria de sistemes lineals invariants en el temps.

En termes generals, si es pot trobar una funció G per a l'operador ${\displaystyle \operatorname {L} }$, aleshores, si multipliquem l'equació (1) per a la funció de Green per f(s), i després integrem respecte a s, obtenim

,$${\displaystyle \int \operatorname {L} \,G(x,s)\,f(s)\,ds=\int \delta (x-s)\,f(s)\,ds=f(x)~.}$$

Perquè l'operador ${\displaystyle \operatorname {L} =\operatorname {L} (x)}$ és lineal i actua només sobre la variable x (i no sobre la variable d'integració s), es pot prendre l'operador ${\displaystyle \operatorname {L} }$ fora de la integració, cedint

$${\displaystyle \operatorname {L} \,\left(\int G(x,s)\,f(s)\,ds\right)=f(x)~.}$$Això vol dir que

és una solució de l'equació ${\displaystyle \operatorname {L} u(x)=f(x)~.}$

Així, es pot obtenir la funció u(x) a través del coneixement de la funció de Green a l'equació (1) i del terme font a la part dreta de l'equació (2). Aquest procés es basa en la linealitat de l'operador ${\displaystyle \operatorname {L} }$.

En altres paraules, la solució de l'equació (2), u(x), es pot determinar mitjançant la integració donada a l'equació (3). Tot i que es coneix f(x), aquesta integració no es pot realitzar a menys que també es conegui G. El problema ara rau a trobar la funció de Green G que satisfà l'equació (1). Per aquest motiu, la funció de Green també s'anomena de vegades la solució fonamental associada a l'operador ${\displaystyle \operatorname {L} }$.

No tots els operadors ${\displaystyle \operatorname {L} }$ admeten una funció de Green. La funció de Green també es pot considerar com una inversa per la dreta de ${\displaystyle \operatorname {L} }$. A part de les dificultats de trobar una funció de Green per a un operador particular, la integral de l'equació (3) pot ser força difícil d'avaluar. Tanmateix, el mètode dóna un resultat teòricament exacte.

Això es pot pensar com una expansió de f segons una base de funció delta de Dirac (projectant f sobre ${\displaystyle \delta (x-s)}$; i una superposició de la solució a cada projecció. Aquesta equació integral es coneix com a equació integral de Fredholm, l'estudi de la qual constitueix la teoria de Fredholm.

L'ús principal de les funcions de Green en matemàtiques és resoldre problemes de valors de contorn no homogenis. En la física teòrica moderna, les funcions de Green també s'utilitzen normalment com a propagadors en diagrames de Feynman; el terme funció de Green s'utilitza sovint per a qualsevol funció de correlació.

Sigui ${\displaystyle \operatorname {L} }$ l'operador de Sturm–Liouville, un operador diferencial lineal de la forma

$${\displaystyle \operatorname {L} ={\dfrac {d}{dx}}\left[p(x){\dfrac {d}{dx}}\right]+q(x)}$$

i sigui ${\displaystyle {\vec {\operatorname {D} }}}$ l'operador de condicions de contorn amb valors vectorials

$${\displaystyle {\vec {\operatorname {D} }}\,u={\begin{bmatrix}\alpha _{1}u'(0)+\beta _{1}u(0)\\\alpha _{2}u'(\ell )+\beta _{2}u(\ell )\end{bmatrix}}~.}$$

Sigui ${\displaystyle f(x)}$ una funció contínua en ${\displaystyle [0,\ell ]\,.}$ Suposem, a més, que el problema

$${\displaystyle {\begin{aligned}\operatorname {L} \,u&=f\\{\vec {\operatorname {D} }}\,u&={\vec {0}}\end{aligned}}}$$

és «regular», és a dir, l'única solució per a ${\displaystyle f(x)=0}$ per a tot x és ${\displaystyle u(x)=0}$.^{[Nota 1]}

Hi ha una i només una solució ${\displaystyle u(x)}$ que satisfà

$${\displaystyle {\begin{aligned}\operatorname {L} \,u&=f\\{\vec {\operatorname {D} }}\,u&={\vec {0}}\end{aligned}}}$$

i ve donada per

$${\displaystyle u(x)=\int _{0}^{\ell }f(s)\,G(x,s)\,ds~,}$$

on ${\displaystyle G(x,s)}$ és una funció de Green que compleix les condicions següents:

1. ${\displaystyle G(x,s)}$ és contínua en ${\displaystyle x}$ i ${\displaystyle s}$.
2. Per a ${\displaystyle x\neq s~}$, ${\displaystyle \quad \operatorname {L} \,G(x,s)=0~}$.
3. Per a ${\displaystyle s\neq 0~}$, ${\displaystyle \quad {\vec {\operatorname {D} }}\,G(x,s)={\vec {0}}~}$.
4. Derivada «salt»: ${\displaystyle \quad G'(s_{0+},s)-G'(s_{0-},s)=1/p(s)~}$.
5. Simetria: ${\displaystyle \quad G(x,s)=G(s,x)~}$.

La funció de Green no és necessàriament única, ja que l'addició de qualsevol solució de l'equació homogènia a una funció de Green dóna lloc a una altra funció de Green. Per tant, si l'equació homogènia té solucions no trivials, existeixen múltiples funcions de Green.

En alguns casos, és possible trobar una funció de Green que només ${\displaystyle s\leq x}$ no s'esvaeix, que s'anomena funció de Green retardada, i una altra funció de Green que només ${\displaystyle s\geq x}$ no s'esvaeix, que s'anomena funció avançada de Green. En aquests casos, qualsevol combinació lineal de les dues funcions de Green també és una funció de Green vàlida.

La terminologia avançada i retardada és especialment útil quan la variable x correspon al temps. En aquests casos, la solució proporcionada per l'ús de la funció de Green retardada depèn només de les fonts passades i és causal, mentre que la solució proporcionada per l'ús de la funció de Green avançada depèn només de les fonts futures i és causal. En aquests problemes, sovint es dóna el cas que la solució causal sigui la físicament important.

L'ús de la funció de Green avançada i retardada és especialment comú per a l'anàlisi de solucions de l'equació d'ones electromagnètiques no homogènies.

Tot i que no soluciona de manera única la forma que prendrà la funció de Green, realitzar una anàlisi dimensional per trobar les unitats que ha de tenir una funció de Green és una comprovació important d'un control de seny de qualsevol funció de Green trobada per altres mitjans. Un examen ràpid de l'equació definidora,

$${\displaystyle LG(x,s)=\delta (x-s),}$$

demostra que les unitats de ${\displaystyle G}$ depenen no només de les unitats de ${\displaystyle L}$, però també sobre el nombre i les unitats de l'espai de què són els vectors de posició ${\displaystyle x}$ i ${\displaystyle s}$ són elements. Això condueix a la relació:

$${\displaystyle [[G]]=[[L]]^{-1}[[dx]]^{-1},}$$

on ${\displaystyle [[G]]}$ es defineix com «les unitats físiques de ${\displaystyle G}$», i ${\displaystyle dx}$ és l'element de volum de l'espai (o espaitemps).

Per exemple, si ${\displaystyle L=\partial _{t}^{2}}$ i el temps és l'única variable, aleshores:

$${\displaystyle [[L]]=[[{\text{temps}}]]^{-2},}$$$${\displaystyle [[dx]]=[[{\text{temps}}]],\ {\text{i}}}$$$${\displaystyle [[G]]=[[{\text{temps}}]].}$$

Si ${\displaystyle L=\square ={\frac {1}{c^{2}}}\partial _{t}^{2}-\nabla ^{2}}$, l'operador de d'Alembert, i l'espai té 3 dimensions llavors:

$${\displaystyle [[L]]=[[{\text{longitud}}]]^{-2},}$$$${\displaystyle [[dx]]=[[{\text{temps}}]][[{\text{longitud}}]]^{3},\ {\text{i}}}$$$${\displaystyle [[G]]=[[{\text{temps}}]]^{-1}[[{\text{longitud}}]]^{-1}.}$$

Si un operador diferencial L admet un conjunt de vectors propis Ψ_n(x) (per exemple, un conjunt de funcions Ψ_n i escalars λ_n tal que LΨ_n = λ_n Ψ_n ) que està complet, llavors és possible construir una funció de Green a partir d'aquests vectors propis i valors propis.

«Complet» significa que el conjunt de funcions {Ψ_n} satisfà la següent relació de completitud,

$${\displaystyle \delta (x-x')=\sum _{n=0}^{\infty }\Psi _{n}^{\dagger }(x)\Psi _{n}(x').}$$

Aleshores es compleix el següent,

${\displaystyle G(x,x')=\sum _{n=0}^{\infty }{\dfrac {\Psi _{n}^{\dagger }(x)\Psi _{n}(x')}{\lambda _{n}}},}$

on ${\displaystyle \dagger }$ representa una conjugació complexa.

L'aplicació de l'operador L a cada costat d'aquesta equació dóna com a resultat la relació de completitud, que es va suposar.

L'estudi general de la funció de Green escrita en la forma anterior, i la seva relació amb els espais funcionals formats pels vectors propis, es coneix com a teoria de Fredholm.

Hi ha diversos altres mètodes per trobar les funcions de Green, inclòs el mètode d'imatges, la separació de variables i les transformades de Laplace.^[1]

Si l'operador diferencial ${\displaystyle L}$ es pot factoritzar com ${\displaystyle L=L_{1}L_{2}}$, llavors la funció de Green ${\displaystyle L}$ es pot construir a partir de les funcions de Green per ${\displaystyle L_{1}}$ i ${\displaystyle L_{2}}$:

$${\displaystyle G(x,s)=\int G_{2}(x,s_{1})\,G_{1}(s_{1},s)\,ds_{1}.}$$

La identitat anterior segueix immediatament de la presa ${\displaystyle G(x,s)}$ per ser la representació de l'operador dret invers de ${\displaystyle L}$, de manera anàloga a l'operador lineal invertible ${\displaystyle C}$, definit per ${\displaystyle C=(AB)^{-1}=B^{-1}A^{-1}}$, es representa pels seus elements matricials ${\displaystyle C_{i,j}}$.

Segueix una identitat addicional per als operadors diferencials que són polinomis escalars de la derivada, ${\displaystyle L=P_{N}(\partial _{x})}$. El teorema fonamental de l'àlgebra, combinat amb el fet que ${\displaystyle \partial _{x}}$ es desplaça amb si mateix, garanteix que el polinomi es pot factoritzar, posant ${\displaystyle L}$ en la forma:

$${\displaystyle L=\prod _{i=1}^{N}(\partial _{x}-z_{i}),}$$

on ${\displaystyle z_{i}}$ són els zeros de ${\displaystyle P_{N}(z)}$. Prenent la transformada de Fourier de ${\displaystyle LG(x,s)=\delta (x-s)}$ respecte a tots dos (${\displaystyle x}$ i ${\displaystyle s}$) obtenim:

$${\displaystyle {\widehat {G}}(k_{x},k_{s})={\frac {\delta (k_{x}-k_{s})}{\prod _{i=1}^{N}(ik_{x}-z_{i})}}.}$$

Aleshores, la fracció es pot dividir en una suma mitjançant una descomposició en fraccions parcials abans de la transformació de Fourier respecte a ${\displaystyle x}$ i ${\displaystyle s}$. Aquest procés produeix identitats que relacionen integrals de les funcions de Green i sumes de les mateixes. Per exemple, si ${\displaystyle L=(\partial _{x}+\gamma )(\partial _{x}+\alpha )^{2}}$ aleshores una forma per a la seva funció de Green és:

$${\displaystyle {\begin{aligned}G(x,s)&={\frac {1}{(\alpha -\gamma )^{2}}}\Theta (x-s)e^{-\gamma (x-s)}-{\frac {1}{(\alpha -\gamma )^{2}}}\Theta (x-s)e^{-\alpha (x-s)}+{\frac {1}{\gamma -\alpha }}\Theta (x-s)\,(x-s)e^{-\alpha (x-s)}\\[5pt]&=\int \Theta (x-s_{1})(x-s_{1})e^{-\alpha (x-s_{1})}\Theta (s_{1}-s)e^{-\gamma (s_{1}-s)}\,ds_{1}.\end{aligned}}}$$

Tot i que l'exemple presentat és tractable analíticament, il·lustra un procés que funciona quan la integral no és trivial (per exemple, quan ${\displaystyle \nabla ^{2}}$ és l'operador del polinomi).

La taula següent ofereix una visió general de les funcions de Green dels operadors diferencials que apareixen amb freqüència, on ${\textstyle r={\sqrt {x^{2}+y^{2}+z^{2}}}}$, ${\textstyle \rho ={\sqrt {x^{2}+y^{2}}}}$, ${\textstyle \Theta (t)}$ és la funció esglaò de Heaviside, ${\textstyle J_{\nu }(z)}$ és una funció de Bessel, ${\textstyle I_{\nu }(z)}$ és una funció de Bessel modificada del primer tipus, i${\textstyle K_{\nu }(z)}$ és una funció de Bessel modificada del segon tipus.^[2] Quan el temps (t) apareix a la primera columna, es mostra la funció avançada (causal) de Green.

Operador diferencial L	Funció de Green G	Exemple d'aplicació
${\displaystyle \partial _{t}^{n+1}}$	${\displaystyle {\frac {t^{n}}{n!}}\Theta (t)}$
${\displaystyle \partial _{t}+\gamma }$	${\displaystyle \Theta (t)e^{-\gamma t}}$
${\displaystyle \left(\partial _{t}+\gamma \right)^{2}}$	${\displaystyle \Theta (t)te^{-\gamma t}}$
${\displaystyle \partial _{t}^{2}+2\gamma \partial _{t}+\omega _{0}^{2}}$ on ${\displaystyle \gamma <\omega _{0}}$	${\displaystyle \Theta (t)e^{-\gamma t}~{\frac {\sin(\omega t)}{\omega }}}$ amb ${\displaystyle \omega ={\sqrt {\omega _{0}^{2}-\gamma ^{2}}}}$	Oscil·lador harmònic 1D subamortit
${\displaystyle \partial _{t}^{2}+2\gamma \partial _{t}+\omega _{0}^{2}}$ on ${\displaystyle \gamma >\omega _{0}}$	${\displaystyle \Theta (t)e^{-\gamma t}~{\frac {\sinh(\omega t)}{\omega }}}$ amb ${\displaystyle \omega ={\sqrt {\gamma ^{2}-\omega _{0}^{2}}}}$	Oscil·lador harmònic 1D subamortit
${\displaystyle \partial _{t}^{2}+2\gamma \partial _{t}+\omega _{0}^{2}}$ on ${\displaystyle \gamma =\omega _{0}}$	${\displaystyle \Theta (t)e^{-\gamma t}t}$	Oscil·lador harmònic 1D amortit
Operador laplacià 2D ${\displaystyle \nabla _{\text{2D}}^{2}=\partial _{x}^{2}+\partial _{y}^{2}}$	${\displaystyle {\frac {1}{2\pi }}\ln \rho }$ amb ${\displaystyle \rho ={\sqrt {x^{2}+y^{2}}}}$	Equació de Poisson 2D
Operador laplacià 3D ${\displaystyle \nabla _{\text{3D}}^{2}=\partial _{x}^{2}+\partial _{y}^{2}+\partial _{z}^{2}}$	${\displaystyle {\frac {-1}{4\pi r}}}$ amb ${\displaystyle r={\sqrt {x^{2}+y^{2}+z^{2}}}}$	Equació de Poisson
Operador de Helmholtz ${\displaystyle \nabla _{\text{3D}}^{2}+k^{2}}$	${\displaystyle {\frac {-e^{-ikr}}{4\pi r}}=i{\sqrt {\frac {k}{32\pi r}}}}$${\displaystyle H_{1/2}^{(2)}(kr)}$${\displaystyle =i{\frac {k}{4\pi }}\,}$${\displaystyle h_{0}^{(2)}(kr)}$; on   ${\displaystyle H_{\alpha }^{(2)}}$ és la funció de Hankel del segon tipus, i,   i   ${\displaystyle h_{0}^{(2)}}$ és la funció de Hankel esfèrica del segon tipus	Equació estacionària de Schrödinger 3D per a una partícula lliure
${\displaystyle \nabla ^{2}-k^{2}}$ en ${\displaystyle n}$ dimensions	${\displaystyle -(2\pi )^{-n/2}\left({\frac {k}{r}}\right)^{n/2-1}K_{n/2-1}(kr)}$	Potencial de Yukawa, propagador de Feynman, equació de Poisson apantallada
${\displaystyle \partial _{t}^{2}-c^{2}\partial _{x}^{2}}$	${\displaystyle {\frac {1}{2c}}\Theta (t-|x/c|)}$	Equació d'ona 1D
${\displaystyle \partial _{t}^{2}-c^{2}\,\nabla _{\text{2D}}^{2}}$	${\displaystyle {\frac {1}{2\pi c{\sqrt {c^{2}t^{2}-\rho ^{2}}}}}\Theta (t-\rho /c)}$	Equació d'ona 2D
Operador de D'Alembert ${\displaystyle \square ={\frac {1}{c^{2}}}\partial _{t}^{2}-\nabla _{\text{3D}}^{2}}$	${\displaystyle {\frac {\delta (t-{\frac {r}{c}})}{4\pi r}}}$	Equació d'ona 3D
${\displaystyle \partial _{t}-k\partial _{x}^{2}}$	${\displaystyle \Theta (t)\left({\frac {1}{4\pi kt}}\right)^{1/2}e^{-x^{2}/4kt}}$	Difusió 1D
${\displaystyle \partial _{t}-k\,\nabla _{\text{2D}}^{2}}$	${\displaystyle \Theta (t)\left({\frac {1}{4\pi kt}}\right)e^{-\rho ^{2}/4kt}}$	Difusió 2D
${\displaystyle \partial _{t}-k\,\nabla _{\text{3D}}^{2}}$	${\displaystyle \Theta (t)\left({\frac {1}{4\pi kt}}\right)^{3/2}e^{-r^{2}/4kt}}$	Difusió 3D
${\displaystyle {\frac {1}{c^{2}}}\partial _{t}^{2}-\partial _{x}^{2}+\mu ^{2}}$	${\displaystyle {\frac {1}{2}}\left[\left(1-\sin {\mu ct}\right)(\delta (ct-x)+\delta (ct+x))+\mu \Theta (ct-|x|)J_{0}(\mu u)\right]}$ amb ${\displaystyle u={\sqrt {c^{2}t^{2}-x^{2}}}}$	Equació de Klein-Gordon 1D
${\displaystyle {\frac {1}{c^{2}}}\partial _{t}^{2}-\nabla _{\text{2D}}^{2}+\mu ^{2}}$	${\displaystyle {\frac {1}{4\pi }}\left[(1+\cos(\mu ct)){\frac {\delta (ct-\rho )}{\rho }}+\mu ^{2}\Theta (ct-\rho )\operatorname {sinc} (\mu u)\right]}$ amb ${\displaystyle u={\sqrt {c^{2}t^{2}-\rho ^{2}}}}$	Equació de Klein-Gordon 2D
${\displaystyle \square +\mu ^{2}}$	${\displaystyle {\frac {1}{4\pi }}\left[{\frac {\delta \left(t-{\frac {r}{c}}\right)}{r}}+\mu c\Theta (ct-r){\frac {J_{1}\left(\mu u\right)}{u}}\right]}$ amb ${\displaystyle u={\sqrt {c^{2}t^{2}-r^{2}}}}$	Equació de Klein-Gordon 3D
${\displaystyle \partial _{t}^{2}+2\gamma \partial _{t}-c^{2}\partial _{x}^{2}}$	${\displaystyle {\frac {1}{2}}e^{-\gamma t}\left[\delta (ct-x)+\delta (ct+x)+\Theta (ct-|x|)\left({\frac {\gamma }{c}}I_{0}\left({\frac {\gamma u}{c}}\right)+{\frac {\gamma t}{u}}I_{1}\left({\frac {\gamma u}{c}}\right)\right)\right]}$ amb ${\displaystyle u={\sqrt {c^{2}t^{2}-x^{2}}}}$	Equacions del telègraf
${\displaystyle \partial _{t}^{2}+2\gamma \partial _{t}-c^{2}\,\nabla _{\text{2D}}^{2}}$	${\displaystyle {\frac {e^{-\gamma t}}{4\pi }}\left[(1+e^{-\gamma t}+3\gamma t){\frac {\delta (ct-\rho )}{\rho }}+\Theta (ct-\rho )\left({\frac {\gamma \sinh \left({\frac {\gamma u}{c}}\right)}{cu}}+{\frac {3\gamma t\cosh \left({\frac {\gamma u}{c}}\right)}{u^{2}}}-{\frac {3ct\sinh \left({\frac {\gamma u}{c}}\right)}{u^{3}}}\right)\right]}$ amb ${\displaystyle u={\sqrt {c^{2}t^{2}-\rho ^{2}}}}$	Conducció de calor relativista 2D
${\displaystyle \partial _{t}^{2}+2\gamma \partial _{t}-c^{2}\,\nabla _{\text{3D}}^{2}}$	${\displaystyle {\frac {e^{-\gamma t}}{20\pi }}\left[\left(8-3e^{-\gamma t}+2\gamma t+4\gamma ^{2}t^{2}\right){\frac {\delta (ct-r)}{r^{2}}}+{\frac {\gamma ^{2}}{c}}\Theta (ct-r)\left({\frac {1}{cu}}I_{1}\left({\frac {\gamma u}{c}}\right)+{\frac {4t}{u^{2}}}I_{2}\left({\frac {\gamma u}{c}}\right)\right)\right]}$ amb ${\displaystyle u={\sqrt {c^{2}t^{2}-r^{2}}}}$	Conducció de calor relativista 3D

Les funcions de Green per a operadors diferencials lineals que impliquen el Laplacià es poden utilitzar fàcilment utilitzant la segona identitat de Green.

Per derivar el teorema de Green, comencem pel teorema de la divergència (també conegut com a teorema de Gauss),

$${\displaystyle \int _{V}\nabla \cdot {\vec {A}}\ dV=\int _{S}{\vec {A}}\cdot d{\widehat {\sigma }}~.}$$

Fem que ${\displaystyle {\vec {A}}=\varphi \,\nabla \psi -\psi \,\nabla \varphi }$ i substituim a la llei de Gauss.

Computem ${\displaystyle \nabla \cdot {\vec {A}}}$ i apliquem la regla del producte per a l'operador ∇,

$${\displaystyle {\begin{aligned}\nabla \cdot {\vec {A}}&=\nabla \cdot (\varphi \,\nabla \psi \;-\;\psi \,\nabla \varphi )\\&=(\nabla \varphi )\cdot (\nabla \psi )\;+\;\varphi \,\nabla ^{2}\psi \;-\;(\nabla \varphi )\cdot (\nabla \psi )\;-\;\psi \nabla ^{2}\varphi \\&=\varphi \,\nabla ^{2}\psi \;-\;\psi \,\nabla ^{2}\varphi .\end{aligned}}}$$

En connectar-ho al teorema de la divergència es produeix el teorema de Green,

$${\displaystyle \int _{V}(\varphi \,\nabla ^{2}\psi -\psi \,\nabla ^{2}\varphi )\,dV=\int _{S}(\varphi \,\nabla \psi -\psi \nabla \,\varphi )\cdot d{\widehat {\sigma }}.}$$

Suposem que l'operador diferencial lineal L és el Laplacià, ∇², i que hi ha una funció de Green G per al Laplacià. La propietat definidora de la funció de Green encara es manté,

$${\displaystyle LG(x,x')=\nabla ^{2}G(x,x')=\delta (x-x').}$$

Sigui ${\displaystyle \psi =G}$ a la segona identitat de Green (vegeu les identitats de Green). Aleshores,

$${\displaystyle \int _{V}\left[\varphi (x')\delta (x-x')-G(x,x')\,{\nabla '}^{2}\,\varphi (x')\right]\ d^{3}x'=\int _{S}\left[\varphi (x')\,{\nabla '}G(x,x')-G(x,x')\,{\nabla '}\varphi (x')\right]\cdot d{\widehat {\sigma }}'.}$$

Amb aquesta expressió, és possible resoldre l'equació de Laplace ∇²φ(x) = 0 o l'equació de Poisson ∇²φ(x) = −ρ(x), subjecte a les condicions de contorn de Neumann o Dirichlet. En altres paraules, podem resoldre per a φ(x) a tot arreu dins d'un volum on (1) el valor de φ(x) s'especifica a la superfície límit del volum (condició de contorn de Dirichlet), o (2) la derivada normal de φ(x) s'especifica a la superfície de límit (condició de contorn de Neumann).

Suposem que el problema és resoldre per φ(x) dins de la regió. Després la integral

$${\displaystyle \int _{V}\varphi (x')\delta (x-x')\,d^{3}x'}$$

es redueix a simplement φ(x) a causa de la propietat definidora de la funció delta de Dirac i tenim

$${\displaystyle \varphi (x)=-\int _{V}G(x,x')\rho (x')\ d^{3}x'+\int _{S}\left[\varphi (x')\,\nabla 'G(x,x')-G(x,x')\,\nabla '\varphi (x')\right]\cdot d{\widehat {\sigma }}'.}$$

Aquesta forma expressa la propietat coneguda de les funcions harmòniques, que si el valor o la derivada normal es coneix en una superfície limitant, llavors el valor de la funció dins del volum es coneix a tot arreu.

En electrostàtica, φ(x) s'interpreta com el potencial elèctric, ρ(x) com la densitat de càrrega elèctrica i la derivada normal ${\displaystyle \nabla \varphi (x')\cdot d{\widehat {\sigma }}'}$ com a component normal del camp elèctric.

Si el problema és resoldre un problema de valors de límit de Dirichlet, la funció de Green s'hauria d'escollir de manera que G(x,x′) s'esvaeixi quan x o x′ es troben a la superfície limitant. Així només queda un dels dos termes de la integral de superfície. Si el problema és resoldre un problema de valor de límit de Neumann, la funció de Green s'escull de manera que la seva derivada normal s'esvaeixi a la superfície limitant, ja que sembla que és l'opció més lògica. Tanmateix, l'aplicació del teorema de Gauss a l'equació diferencial que defineix la funció de Green produeix

$${\displaystyle \int _{S}\nabla 'G(x,x')\cdot d{\widehat {\sigma }}'=\int _{V}\nabla '^{2}G(x,x')d^{3}x'=\int _{V}\delta (x-x')d^{3}x'=1~,}$$

és a dir, la derivada normal de G(x,x′) no pot desaparèixer a la superfície, perquè s'ha d'integrar a 1 a la superfície.

La forma més simple que pot adoptar la derivada normal és la d'una constant, és a dir, 1/S, on S és l'àrea superficial de la superfície. El terme «superficial» de la solució esdevé$${\displaystyle \int _{S}\varphi (x')\,\nabla 'G(x,x')\cdot d{\widehat {\sigma }}'=\langle \varphi \rangle _{S}}$$

on ${\displaystyle \langle \varphi \rangle _{S}}$ és el valor mitjà del potencial a la superfície. Aquest nombre no es coneix en general, però sovint no té importància, ja que sovint l'objectiu és obtenir el camp elèctric donat pel gradient del potencial, més que el potencial en si.

Sense condicions de límit, la funció de Green per al Laplacià (funció de Green per a l'equació de Laplace de tres variables) és

$${\displaystyle G(x,x')=-{\dfrac {1}{4\pi |x-x'|}}.}$$

Suposant que la superfície de delimitació surt a l'infinit i connectant aquesta expressió per a la funció de Green, finalment es produeix l'expressió estàndard per al potencial elèctric en termes de densitat de càrrega elèctrica com

${\displaystyle \varphi (x)=\int _{V}{\dfrac {\rho (x')}{4\pi \varepsilon |x-x'|}}\,d^{3}x'~.}$

Trobeu la funció de Green per al problema següent, el número de la funció de Green és X11:

$${\displaystyle {\begin{aligned}Lu&=u''+k^{2}u=f(x)\\u(0)&=0,\quad u\left({\tfrac {\pi }{2k}}\right)=0.\end{aligned}}}$$

Primer pas: La funció de Green per a l'operador lineal en qüestió es defineix com la solució a

Si ${\displaystyle x\neq s}$, aleshores la funció delta dóna zero, i la solució general és

$${\displaystyle G(x,s)=c_{1}\cos kx+c_{2}\sin kx.}$$

Per a ${\displaystyle x<s}$, la condició d'entorn a ${\displaystyle x=0}$ implica

$${\displaystyle G(0,s)=c_{1}\cdot 1+c_{2}\cdot 0=0,\quad c_{1}=0}$$

Si ${\displaystyle x<s}$ i ${\displaystyle s\neq {\tfrac {\pi }{2k}}}$.

Per a ${\displaystyle x>s}$, la condició d'entorn a ${\displaystyle x={\tfrac {\pi }{2k}}}$ implica

$${\displaystyle G\left({\tfrac {\pi }{2k}},s\right)=c_{3}\cdot 0+c_{4}\cdot 1=0,\quad c_{4}=0}$$

L'equació de ${\displaystyle G(0,s)=0}$ s'omet per motius similars.

Per resumir els resultats fins ara:

$${\displaystyle G(x,s)={\begin{cases}c_{2}\sin kx,&{\text{per a }}x<s,\\c_{3}\cos kx,&{\text{per a }}s<x.\end{cases}}}$$

Segon pas: La següent tasca és determinar ${\displaystyle c_{2}}$ i ${\displaystyle c_{3}}$.

Garantir la continuïtat en la funció de Green a ${\displaystyle x=s}$ implica

$${\displaystyle c_{2}\sin ks=c_{3}\cos ks}$$

Es pot assegurar una discontinuïtat adequada en la primera derivada integrant l'equació diferencial definidora (és a dir, Eq. *) de ${\displaystyle x=s-\varepsilon }$ a ${\displaystyle x=s+\varepsilon }$ i prenent el límit com 𝜀 va a zero. S'ha de tenir en compte que només integrem la segona derivada ja que el terme restant serà continu per construcció.$${\displaystyle c_{3}\cdot (-k\sin ks)-c_{2}\cdot (k\cos ks)=1}$$

Es poden resoldre les dues equacions de (dis)continuïtat ${\displaystyle c_{2}}$ i ${\displaystyle c_{3}}$ per obtenir

$${\displaystyle c_{2}=-{\frac {\cos ks}{k}}\quad ;\quad c_{3}=-{\frac {\sin ks}{k}}}$$

Així que la funció de Green per a aquest problema és:

$${\displaystyle G(x,s)={\begin{cases}-{\frac {\cos ks}{k}}\sin kx,&x<s,\\-{\frac {\sin ks}{k}}\cos kx,&s<x.\end{cases}}}$$

• Sigui n = 1 i que el subconjunt sigui tot R. Sigui L sent ${\textstyle {\frac {d}{dx}}}$. Aleshores, la funció esglaó de Heaviside H(x − x₀) és una funció de Green de L en x₀.
• Sigui n = 2 i fem que el subconjunt sigui el mig semiplà {(x, y) : x, y ≥ 0} i L sigui el Laplacià. A més, suposem que una condició de contorn de Dirichlet s'imposa a x = 0 i una condició de contorn de Neumann s'imposa a y = 0. Aleshores la funció de X10Y20 de Green és$${\displaystyle {\begin{aligned}G(x,y,x_{0},y_{0})={\dfrac {1}{2\pi }}&\left[\ln {\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}}}-\ln {\sqrt {(x+x_{0})^{2}+(y-y_{0})^{2}}}\right.\\[5pt]&\left.{}+\ln {\sqrt {(x-x_{0})^{2}+(y+y_{0})^{2}}}-\ln {\sqrt {(x+x_{0})^{2}+(y+y_{0})^{2}}}\,\right].\end{aligned}}}$$
• Sigui ${\displaystyle a<x<b}$, i tots tres són elements dels nombres reals. Aleshores, per a qualsevol funció ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ amb una 𝑛-èsima derivada que és integrable en l'interval ${\displaystyle [a,b]}$: $${\displaystyle {\begin{aligned}f(x)&=\sum _{m=0}^{n-1}{\frac {(x-a)^{m}}{m!}}\left[{\frac {d^{m}f}{dx^{m}}}\right]_{x=a}+\int _{a}^{b}\left[{\frac {(x-s)^{n-1}}{(n-1)!}}\Theta (x-s)\right]\left[{\frac {d^{n}f}{dx^{n}}}\right]_{x=s}ds\end{aligned}}~.}$$La funció de Green a l'equació anterior, ${\displaystyle G(x,s)={\frac {(x-s)^{n-1}}{(n-1)!}}\Theta (x-s)}$, no és únics. Com es modifica l'equació si ${\displaystyle g(x-s)}$ s'afegeix a ${\displaystyle G(x,s)}$, on ${\displaystyle g(x)}$ satisfà ${\textstyle {\frac {d^{n}g}{dx^{n}}}=0}$ per a tot ${\displaystyle x\in [a,b]}$ (per exemple, ${\displaystyle g(x)=-x/2}$ amb ${\displaystyle n=2}$) . A més, compareu l'equació anterior amb la forma d'una sèrie de Taylor centrada en ${\displaystyle x=a}$.

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Funció de Green